|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Конечных приращений формула | Конечных приращений формула (далее К) формула Лагранжа, одна из основных формул дифференциального исчисления, дающая связь между приращением функции f(x) и значениями ее производной, эта формула имеет вид:
f(b)-f(a)=(b-a)f`(c), (1)
где с — некоторое число, удовлетворяющее неравенствам a<с<b. Формула (1) справедлива, если функция f(x) непрерывна на отрезке (a,b) и имеет производную в каждой точке интервала (а, b). Геометрически формула (1) выражает, что на кривой y = f(x) найдется точка (c, f(c)), касательная в которой параллельна хорде, проходящей через точки (a, f(a)) и (b, f(b)). К была открыта Ж. Лагранжем в 1797.
Среди различных обобщений К следует отметить формулу Бонне
 ,
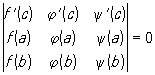ее частный случай — формулу Коши
 .
|
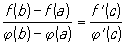Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 27.02.2025 22:57:53
|
|
|
|
|
|
|
|
|
|
|
