
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Комплексная амплитуда | Комплексная амплитуда (далее К) представление амплитуды А и фазы y гармонического колебания х = Acos (wt + y) с помощью комплексного числа 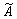 =Aexp (ij)=Acosj + iAsinj. При этом гармоническое колебание описывается выражением х = ( =Aexp (ij)=Acosj + iAsinj. При этом гармоническое колебание описывается выражением х = (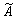 (expiwt)), где - вещественная часть комплексного числа, стоящего в квадратных скобках. К обычно применяются при расчете линейных электрических цепей (с линейной зависимостью тока от напряжений), содержащих активные и реактивные элементы. Если на такую цепь действует гармоническая эдс частоты w, то использование К тока и напряжения позволяет перейти от дифференциальных уравнений к алгебраическим. Связь между К тока и напряжения для активного сопротивления R определяется законом Ома: / = (expiwt)), где - вещественная часть комплексного числа, стоящего в квадратных скобках. К обычно применяются при расчете линейных электрических цепей (с линейной зависимостью тока от напряжений), содержащих активные и реактивные элементы. Если на такую цепь действует гармоническая эдс частоты w, то использование К тока и напряжения позволяет перейти от дифференциальных уравнений к алгебраическим. Связь между К тока и напряжения для активного сопротивления R определяется законом Ома: / =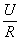 · R. Для индуктивности L эта связь имеет вид = · R. Для индуктивности L эта связь имеет вид =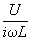 - а для емкости С: =iw. Таким образом, величины iwL и L/iw играют роли индуктивного и емкостного сопротивлений. - а для емкости С: =iw. Таким образом, величины iwL и L/iw играют роли индуктивного и емкостного сопротивлений.
Расчет К тока для участка электрической цепи, содержащего элементы L, С и R, на который действует внешняя гармоническая эдс частоты w, производится с помощью соотношения, аналогичного закону Ома: /= 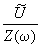 . Здесь Z - комплексное сопротивление данного участка цепи, которое может быть найдено по тем же правилам последовательного и параллельного включения сопротивлений, что и для цепей из активных сопротивлений на постоянном токе. Найденная таким образом К тока позволяет определить амплитуду и фазу реального тока, протекающего в цепи. . Здесь Z - комплексное сопротивление данного участка цепи, которое может быть найдено по тем же правилам последовательного и параллельного включения сопротивлений, что и для цепей из активных сопротивлений на постоянном токе. Найденная таким образом К тока позволяет определить амплитуду и фазу реального тока, протекающего в цепи.
Метод К может быть применен при любом периодическом воздействии на линейную цепь. При этом внешнее негармоническое воздействие должно быть разложено в ряд Фурье, после чего производится расчет цепи для каждой из компонент внешнего воздействия и суммирование полученных результатов. При расчете методом К средней мощности Р =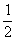 IUcosj, где j - сдвиг фаз между током и напряжением, необходимо пользоваться правилом: активная мощность равна Р= IUcosj, где j - сдвиг фаз между током и напряжением, необходимо пользоваться правилом: активная мощность равна Р= 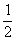 ·(*+*). ·(*+*).
Здесь /* и * - комплексно сопряженные амплитуды тока и напряжения.
В. Н. Парыгин. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:42:53
|

|

|
 |
|

|
 |
 |
 |
|