|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Клейна - Гордона уравнение | Клейна - Гордона уравнение (далее К)квантовое релятивистское (т. е. удовлетворяющее требованиям относительности теории) уравнение для частиц со спином нуль. Исторически К. - Г. у. было первым релятивистским уравнением квантовой механики для волновой функции частицы y; оно было предложено в 1926 Э. Шредингером (как релятивистское обобщение Шредингера уравнения) и независимо от него шведским физиком О. Клейном (О. Klein), советским физиком В. А. Фоком, немецким физиком В. Гордоном (. Gordon) и др.
Для свободной частицы К. - Г. у. записывается в виде:
 .
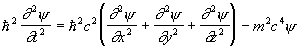Ему соответствует релятивистское соотношение между энергией E и импульсом р частицы: 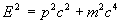 (m - масса частицы, с - скорость света).
Решением уравнения является функция y (х, у, z, t), зависящая только от координат (х, у, z) и времени (t). Следовательно, частицы, описываемые этой функцией, не обладают никакими дополнительными внутренними степенями свободы, т. е. действительно являются бесспиновыми (к таким частицам относятся, например, p- и К-мезоны). Однако анализ уравнения показал, что его решение y принципиально отличается по своему физическому смыслу от обычной волновой функции как амплитуды вероятности обнаружить частицу в заданном месте пространства в заданный момент времени: y (х, у, z, t) не определяется однозначно значением y в начальный момент времени (такая однозначная зависимость постулируется в квантовой механике), и, более того, выражение для вероятности данного состояния наряду с положительными значениями может принимать также и лишенные физического смысла отрицательные значения. Поэтому сначала от К. - Г. у. отказались. Однако в 1934 В. Паули и В. Вайскопф нашли правильную интерпретацию этого уравнения в рамках квантовой теории поля (они рассмотрели его как уравнение поля, аналогичное Максвелла уравнениям для электромагнитного поля, и проквантовали его; при этом y стало оператором).
М. А. Либерман. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 31.10.2025 10:49:41
|
|
|
|
|
|
|
|
|
|
|
