|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Класс (в логике) | Класс (далее К) (в логике), понятие, выражающее совокупность (множество) предметов, удовлетворяющих каким-либо условиям или признакам (иногда различают понятия "К (в логике)" и "множество", что бывает связано со специальными вопросами множеств теории); про такие предметы говорят, что они являются элементами (данного) К (в логике) (отношение принадлежности элемента классу обозначается обычно знаком Î; запись аÎА читается: "а есть элемент класса А"). Предполагается, что в связи с каждым свойством (понятием о свойстве) можно рассматривать К (в логике) предметов, имеющих это свойство (например, свойству быть четным числом соответствует К (в логике) всех четных чисел). К (в логике) соответствующий некоторому свойству, может состоять из любого конечного числа предметов (конечные К (в логике) часто задаются перечнем своих элементов - списком их названий); он может быть бесконечным (например, упомянутый К (в логике) всех четных чисел) или пустым (т. е. вовсе не содержать элементов; пустой К (в логике) обычно обозначается Î или Æ). К (в логике), состоящий только из одного элемента, называется единичным, или сингулярным (сингулярные и пустые К (в логике) Аристотель не вводил при построении своей силлогики; см. Силлогизм). Пустому К (в логике) противополагается универсальный К (в логике) (обозначается ), уточняющий круг исследуемых предметов и состоящий из всех объектов подлежащей рассмотрению предметной области. Геометрический К (в логике) изображаются обычно фигурами, ограниченными простыми замкнутыми кривыми (например, окружностями на плоскости). Рассматриваются операции над К (в логике) и отношения между К (в логике) Операции над К (в логике): пересечение классов А и В - класс (обычное обозначение: АÇВ), состоящий из всех тех, и только тех элементов, которые содержатся в обоих классах А и В; объединение классов А и В - класс (AÈВ), состоящий из всех тех, и только тех элементов, которые содержатся хотя бы в одном из классов А или В; дополнение класса А - класс 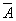 , состоящий из всех тех, и только тех предметов универсального К (в логике), которые не входят в класс А. Отношения между (двумя произвольными) К (в логике): тождественности (совпадения); включения - один К (в логике) является частью (подклассом) другого; частичного совпадения (когда К (в логике) имеют хотя бы один общий элемент) и исключения (когда они не имеют общих элементов). Изучение свойств операций над К (в логике) и отношений между К (в логике) проводится в логике классов.
Лит.: Гильберт Д., Аккерман В., Основы теоретической логики, пер. с нем., М., 1947; Тарский А., Введение в логику и методологию дедуктивных наук, пер. с англ., М., 1948; Яновская С. А., Логика классов, в кн.: Философская энциклопедия, т. 3, М., 1964; Кузичев А. С., Диаграммы Венна, М., 1968; Мендельсон Э., Введение в математическую логику, пер. с англ., М., 1971.
А. С. Кузичев. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 23.12.2024 02:10:18
|
|
|
|
|
|
|
|
|
|
|
