Кинетика физическая

Кинетика физическая (далее К) теория неравновесных макроскопических процессов, то есть процессов, возникающих в системах, выведенных из состояния теплового (термодинамического) равновесия. К К можно отнести термодинамику неравновесных процессов, кинетическую теорию газов (в том числе плазмы), теорию процессов переноса в твердых телах, а также общую статистическую теорию неравновесных процессов, которая начала развиваться лишь в 50-е гг.

Все неравновесные процессы в адиабатически изолированных системах (системах, не обменивающихся теплом с окружающими телами) являются необратимыми процессами — происходят с увеличением энтропии; в равновесном состоянии энтропия достигает максимума.

Как и в случае равновесных состояний, в К возможны два способа описания систем: феноменологический, или термодинамический (термодинамика неравновесных процессов), и статистический.

Термодинамический метод описания неравновесных процессов

При термодинамическом описании неравновесных процессов рассматривается изменение в пространстве и времени таких макроскопических параметров состояния системы, как плотность массы i-го компонента r_i(r, t), плотность импульса ru (r, t), локальная температура T (r, t), поток массы i-го компонента j_i(r, t), плотность потока внутренней энергии q (r, t) (здесь r — координата, t — время, u — средняя массовая скорость, r — плотность массы). В равновесном состоянии системы r, r_i, Т постоянны, а потоки равны нулю.

Термодинамическое описание неравновесных возможно лишь при достаточно медленном параметров состояния в пространстве и во времени для состояний, близких к равновесным. Для газов это означает, что все термодинамические параметры, характеризующие состояние системы, мало меняются на длине свободного пробега и за время, равное среднему времени свободного пробега молекул (среднему времени между двумя последовательными столкновениями молекул). Медленные процессы встречаются практически очень часто, так как установление равновесия происходит только после очень большого числа столкновений; к ним относятся: диффузия, теплопроводность, электропроводность и т.д. Отклонения от состояния термодинамического равновесия характеризуются градиентами температуры, концентрации (r_i/r) и массовой скорости (так называемыми термодинамическими силами), а потоки энергии, массы i-го компонента и импульса связаны с термодинамическими силами линейными соотношениями. Коэффициенты в этих соотношениях называются кинетическими коэффициентами.

Рассмотрим в качестве примера диффузию в бинарной смеси, то есть процесс выравнивания концентрации компонентов в результате хаотического теплового движения молекул. Феноменологическое уравнение, описывающее процесс диффузии, получают с помощью закона сохранения вещества и того опытного факта, что поток вещества одного из компонентов вследствие диффузии прямо пропорционален градиенту его концентрации (с обратным знаком). Коэффициент пропорциональности называется коэффициентом диффузии. Согласно уравнению диффузии, скорость изменения концентрации вещества со временем прямо пропорциональна дивергенции градиента концентрации с коэффициентом пропорциональности, равным коэффициенту диффузии.

Решение уравнения диффузии позволяет определить время, в течение которого произойдет выравнивание концентрации молекул в системе (например, в сосуде с газом) за счет диффузии (время релаксации). Время релаксации t_р имеет порядок: t_р ~ L²/D, где L — линейные размеры сосуда, a D — коэффициент диффузии. Это время тем больше, чем больше размеры сосуда и чем меньше коэффициент диффузии. Коэффициент диффузии пропорционален длине свободного пробега молекул l и их средней тепловой скорости n. Поэтому время релаксации оказывается пропорциональным: t_р ~ L²/ ln = (L/l)²l/n, где l/n = t — среднее время свободного пробега. Очевидно, что t_р >> t при L >> l. Таким образом, условие L >> l (размеры системы велики по сравнению с длиной свободного пробега молекул) является необходимым для того, чтобы процесс установления равновесного состояния можно было считать медленным. Аналогичным образом устанавливаются уравнения, описывающие теплопроводность, внутреннее трение, электропроводность и т.д. Коэффициент диффузии, теплопроводности и вязкости, а также удельная электропроводность в феноменологической теории должны быть определены экспериментально.

Перечисленные процессы называются прямыми. Этим подчеркивается, что, например, при диффузии градиент концентрации данного вещества вызывает поток этого же вещества; градиент температуры вызывает поток внутренней энергии, которая при постоянной концентрации молекул меняется только с температурой; электрический ток вызывается градиентом потенциала и т.д. Кроме прямых процессов, существуют еще так называемые перекрестные процессы. Примером перекрестного процесса может служить термодиффузия — перенос вещества не вследствие градиента концентрации (это была бы обычная диффузия), а вследствие градиента температуры. Термодиффузия создает градиент концентрации, что приводит к появлению обычной диффузии. Если разность температур в системе поддерживается постоянной, то устанавливается стационарное состояние, при котором потоки вещества, вызванные градиентами температуры и концентрации, взаимно уравновешиваются. В смеси газов при этом концентрация молекул в местах повышенной температуры оказывается большей для молекул меньшей массы (данное явление используется для разделения изотопов).

Градиент концентрации в свою очередь создает поток внутренней энергии. В этом состоит процесс диффузионной теплопроводности. При наличии в теле заряженных частиц градиент температуры создает упорядоченное перемещение этих частиц — электрический ток, называемый термоэлектрическим (см. Термоэлектрические явления).

В К важное значение имеет принцип симметрии кинетических коэффициентов, установленный Л. Онсагером. В равновесном состоянии термодинамические параметры a_i (давление, температура и т.д.), характеризующие состояние макроскопической системы, постоянны во времени: da_i/dt = 0. Важнейшая функция состояния системы — энтропия , зависящая от a_i, в состоянии равновесия имеет максимум и, следовательно, ее частные производные ¶/¶_aj = 0. При малом отклонении системы от равновесия производные ¶/¶_aj и ¶a/¶t малы, но отличны от нуля, и между ними существуют приближенные линейные соотношения. Коэффициенты пропорциональности в этих соотношениях и есть кинетические коэффициенты. Если через g_ik обозначить коэффициент, определяющий скорость изменения параметра системы a_i зависимости от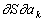

, то, согласно принципу Онсагера (в отсутствие поля и вращения системы как целого), имеет место равенство g_ik = g_ki. Принцип Онсагера вытекает из свойства микроскопической обратимости, которая выражается в инвариантности уравнений движения частиц системы относительно замены знака времени: t ® —t (см. Онсагера теорема). Из этого принципа, в частности, следует существование связи между коэффициентами, определяющим выделение током тепла из-за неравномерного нагрева проводника (Томсона эффект), и коэффициентами, определяющим выделение током тепла в спаях разнородных проводников или полупроводников (Пельтье эффект).

Статистический метод описания неравновесных процессов.

Статистическая теория неравновесных процессов является более детальной и глубокой, чем термодинамическая. В отличие от термодинамического метода, статистическая теория на основе определенных представлений о строении вещества и действующих между молекулами силах позволяет вычислить кинетические коэффициенты, определяющие интенсивность процессов диффузии, внутреннего трения (вязкости), электропроводности и т.д. Однако эта теория весьма сложна.

Статистический метод описания систем как в равновесном, так и неравновесном состоянии основан на вычислении функции распределения. Для равновесных состояний имеются универсальные функции распределения координат и импульсов (или скоростей) всех частиц, определяющие вероятность того, что эти величины принимают фиксированные значения. Для систем, находящихся в тепловом контакте с окружающей средой, температура которой постоянна, это — каноническое Гиббса распределение, а для изолированных систем — микроканоническое Гиббса распределение; оба распределения полностью определяются энергией системы.

Неравновесные состояния в гораздо большей степени (чем равновесные) зависят от микроскопических свойств систем: свойств и молекул и сил взаимодействия между ними. Лишь в 50—60-е гг. были разработаны общие методы построения функций распределения (по координатам и импульсам всех частиц системы), аналогичных каноническому распределению Гиббса, но описывающих неравновесные процессы.

С помощью функций распределения можно определить любые макроскопические величины, характеризующие состояние системы, и проследить за их изменением в пространстве с течением времени. Это достигается вычислением статистических средних (см. Статистическая физика). Нахождение функции распределения, зависящей от координат и импульсов всех частиц, является в общем случае неразрешимой задачей, т.к. оно эквивалентно решению уравнений движения для всех частиц системы. Однако для практических целей нет необходимости в знании точного вида этой функции распределения: она содержит слишком подробную информацию о движении отдельных частиц, которая не существенна для определения поведения системы в целом. В связи с этим используется приближенное статистическое описание с помощью более простых функций распределения. Для описания состояния газов средней плотности достаточно знания так называемой одночастичной функции распределения f (p, r, t), дающей среднее число частиц с определенными значениями импульсов р (или скоростей n) и координат r. Для газов более высокой плотности необходимо знание двухчастичных (парных) функций распределения. Общий метод получения уравнений для одночастичных и более сложных функций (зависящих от координат и импульсов двух и более частиц) был разработан Н. Н. Боголюбовым, М. Борном, М. Грином и др. Эти уравнения называются кинетическими. К их числу относится кинетическое уравнение Больцмана для разреженных газов, полученное Л. Больцманом из соображений, основанных на балансе частиц со скоростями в интервалах Dn_x, Dn_y, Dn_z внутри объема Dх Dy Dz (n_x, n_y, n_z— проекции скорости n на координатные оси х, у, z). Разновидностями уравнения Больцмана для ионизированного газа (плазмы) являются кинетические уравнения Л. Д. Ландау и А. А. Власова (см. Плазма).

Кинетические уравнения могут быть построены не только для газов, но и для малых возбуждений в конденсированных системах. Тепловое движение системы характеризуется различного рода возбуждениями. В газе это — поступательное движение составляющих его частиц и внутренние возбуждения и молекул. В общем случае тепловое движение характеризуется возбуждениями более сложной природы. Так, в телах тепловое возбуждение можно представить в виде упругих волн, распространяющихся вдоль точнее — волн, соответствующих нормальным колебаниям кристаллической решетки. В плазме коллективными возбуждениями являются колебания плотности электрического заряда, вызванные дальнодействующими кулоновскими силами. В металлах возможны электронные возбуждения (переходы электронов из состояний внутри Ферми поверхности в состояния вне ее), а в полупроводниках — еще и дырочные возбуждения (появление свободных от электронов состояний в валентной зоне при переходе электронов в зону проводимости; см. Полупроводники). При низких температурах, в слабовозбужденном состоянии, энергию возбуждения всегда можно представить в виде суммы некоторых элементарных возбуждений, или, на квантовом языке, квазичастиц. Понятие о квазичастицах применимо не только для тел, но и для жидких, газообразных и аморфных, если температура не слишком велика. Функции распределения для квазичастиц системы, находящейся в неравновесном состоянии, удовлетворяют кинетическому уравнению.

В случае квантовых систем функция распределения зависит от спина частиц (или квазичастиц). В частности, для частиц с полуцелым спином равновесной функцией распределения служит распределение — Дирака, а для частиц (квазичастиц) с целым или нулевым спином — распределение Бозе — Эйнштейна (см. Статистическая физика).

В кинетических уравнениях наряду с внешними воздействиями учитываются взаимодействия между частицами или квазичастицами, причем эти взаимодействия рассматриваются как парные столкновения. Именно эти взаимодействия приводят к установлению равновесных состояний. Во многих случаях функция распределения не зависит явно от времени. Такая функция называется стационарной, она описывает процессы, течение которых не претерпевает изменений со временем. При стационарных процессах изменение функции распределения вследствие внешних воздействий компенсируется ее изменением в результате столкновений.

В простых случаях можно грубо оценить изменение функции распределения f системы в результате столкновений, считая, что оно пропорционально величине отклонения от равновесной функции (так как только при отклонении от состояния равновесия столкновения меняют функцию распределения). Величина, обратная коэффициенту пропорциональности в этом соотношении, называется временем релаксации. В общем случае учесть взаимодействие таким простым способом невозможно, и в кинетическое уравнение входит так называемый интеграл столкновений, который более точно учитывает результат изменения функции распределения вследствие взаимодействия частиц (квазичастиц).

Решая кинетическое уравнение, находят неравновесную функцию распределения и вычисляют потоки энергии, массы и импульса, что позволяет получить уравнения теплопроводности, диффузии и переноса импульса (уравнение Навье — Стокса) с кинетическими коэффициентами, выраженными через молекулярные постоянные. (Однако кинетическое уравнение можно построить лишь для газов (из частиц или квазичастиц)).

Основные принципы теории неравновесных процессов надежно установлены. Разработаны методы построения уравнений переноса энергии, массы и импульса в различных системах, не только в газах, а, например, и в жидкостях. При этом получают выражения для кинетических коэффициентов, входящих в эти уравнения, через корреляционные функции (функции, описывающие корреляцию в пространстве и во времени) потоков этих физических величин, то есть в конечном счете, через молекулярные постоянные. Эти выражения очень сложны и могут быть вычислены лишь средствами современной вычислительной математики.

Лит.: Гуревич Л. Э., Основы физической кинетики, М.— Л., 1940; Боголюбов Н. Н., Проблемы динамической теории в статистической физике, М.—Л., 1946; Гуров К. П,, Основания кинетической теории. Метод Н. Н. Боголюбова, М., 1966; Ландау Л. Д., Лифшиц Е. М., Статистическая физика, М., 1964 (Теоретическая физика, т. 5): Климонтович Ю. Л., Статистическая теория неравновесных процессов в плазме, М., 1964; Пригожин И. Р., Неравновесная статистическая механика, пер. с англ., М., 1964; Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971; Гроот С., Мазур П., Неравновесная термодинамика, пер. с англ., М., 1964; Честер Дж., Теория необратимых процессов, пер. с англ., М., 1966; Хаазе Р., Термодинамика необратимых процессов, пер. с нем., М., 1967.

Г. Я. Мякишев.

		Новости 05.11.2024 17:02:57

	Copyright © 1999-2024 Oval.ru, All Rights Reserved.