
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Кеплера законы | Кеплера законы (далее К) три закона движения планет, открытые И. Кеплером в начале 17 в. Основной труд Кеплера "Новая астрономия", напечатанный в 1609, содержал два первых закона. Третий закон был открыт позднее: в 3-й главе 5-й книги "Гармония Мира" (1619) Кеплер отметил, что идея нового закона блеснула у него внезапно 8 марта 1618 года, а 15 мая он закончил все необходимые вычисления, которые показали, что закон верен. В дальнейшем К уточнялись и окончательно получили следующую формулировку.
Первый К В невозмущенном движении (т. е. в задаче двух тел) орбита движущейся точки есть кривая второго порядка, в одном из фокусов которой находится центр силы притяжения. Таким образом, орбита материальной точки в невозмущенном движении — это некоторое коническое сечение, то есть окружность, эллипс, парабола или гипербола. Второй К В невозмущенном движении площадь, описываемая радиус-вектором движущейся точки, изменяется пропорционально времени. Первые два К имеют место только для невозмущенного движения, происходящего под действием силы притяжения, обратно пропорциональной квадрату расстояния до центра силы. Третий К В невозмущенном эллиптическом движении двух материальных точек произведение квадратов времен обращения на суммы масс центральной и движущейся точек как кубы больших полуосей их орбит, т. е.
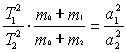 , ,
где Т1 и Т2 — периоды обращения двух точек, m1 и m2 — их массы, m0 — масса центральной точки, a1 и а2 — большие полуоси орбит точек. Пренебрегая массами планет по сравнению с массой Солнца, получаем третий К в его первоначальной форме: квадраты периодов обращений двух планет вокруг Солнца относятся как кубы больших полуосей их эллиптических орбит. Третий К может быть применен только для случая эллиптических орбит, а поэтому не имеет такого общего значения, как два первых закона. Однако, будучи применен к планетам, спутникам планет, компонентам двойных звезд, движущимся по эллиптическим орбитам, он позволяет определить некоторые характеристики небесных светил. Так, на основании третьего К возможно подсчитать массы планет, принимая массу Солнца m0 = 1. Зная из наблюдений период обращения одного компонента двойной звезды относительно другого и измерив ее параллакс, можно найти сумму их масс. Если параллаксы звезд неизвестны, то на основании допущения, что массы компонентов соответствуют их физическим особенностям, по третьему К можно вычислить расстояния до звезд (это так называемы динамические параллаксы звезд).
Открыв первые два закона, Кеплер составил основанные на них таблицы движения планет, опубликованные в 1627 под названием "Рудольфовых таблиц". Эти таблицы по своей точности далеко превзошли все прежние, ими пользовались в практической астрономии на протяжении 17 и 18 вв. Успех Кеплера в объяснении движения планет обусловлен новым методологическим подходом к решению вопроса: впервые в истории астрономии была сделана попытка определить планетные орбиты непосредственно из наблюдений.
Уже Кеплеру было ясно, что открытые им законы не являются совершенно строгими. Если для планет они выполняются с большой точностью, то для того, чтобы представить движение Луны, оказалось необходимым ввести эллипс с вращающейся линией апсид и добавить неравенства, называемые эвекцией и вариацией. Эти неравенства были открыты эмпирически еще Птолемеем во 2 в. (эвекция) и Т. Браге в 16 в. (вариация) и объяснены только после открытия в 17 в. И. Ньютоном закона всемирного тяготения (см. Ньютона закон тяготения). К, найденные из наблюдений, были выведены Ньютоном как строгое решение задачи двух тел.
Лит.: Дубошин Г. Н., Небесная механика. Основные задачи и методы, 2 изд., М., 1968: Субботин М. Ф., Введение в теоретическую астрономию, М., 1968; Рябов Ю. А., К 350-летию открытия первых двух законов Кеплера, в кн.: Астрономический календарь на 1959, М., 1958.
Г. А. Чеботарев. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:40:01
|

|

|
 |
|

|
 |
 |
 |
|