Квантор

Квантор (далее К) (от лат. quantum — сколько), логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате ее применения. В обычном языке носителями таких характеристик служат слова типа "все", "каждый", "некоторый", "существует", "имеется", "любой", "всякий", "единственный", "несколько", "бесконечно много", "конечное число", а также все количественные числительные. В формализованных языках, составной частью которых является исчисление предикатов, для выражения всех подобных характеристик оказывается достаточным К двух видов: К (все) общности (оборот "для всех х", обозначается через "x, ("x), (x) (Ax), 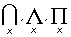) и К существования ("для некоторых х", обозначения: $x, ($x), (Ех), 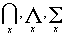С помощью К можно записать четыре основных формы суждений традиционной логики: "все А суть В" записывается в виде "x (A (x)É É (x)), "ни одно A не есть " — в виде "x (A (x)É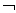 (x)), "некоторые А суть " — в виде $x (A (x)& (x)), "некоторые А не суть В" — в виде $x (A (x)& 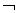(x)) (здесь А (х) означает, что х обладает свойством A, É — знак импликации,  — отрицания, & — конъюнкции).   Часть формулы, на которую распространяется действие каких-либо К, называется областью действия этого К (ее можно указать с помощью скобок). Вхождение какой-либо переменной в формулу непосредственно после знака К или в область действия К, после которого стоит эта переменная, называется ее связанным вхождением. Все остальные вхождения переменных называются свободными. Формула, содержащая свободные вхождения переменных, зависит от них (является их функцией); связанные же вхождения переменных можно "переименовывать"; например, записи $x (x = 2y) и $z (z = 2y) означают одно и то же, чего нельзя сказать о $x (x = 2y) и $x (x = 2t). Применение К уменьшает число свободных переменных в логическом выражении и превращает (если К не "фиктивный", т. е. относится к переменной, действительно входящей в формулу) трехместный предикат в двухместный, двухместный — в одноместный, одноместный — в высказывание. Употребление К кодифицируется специальными "постулатами квантификации" (присоединение которых к исчислению высказываний по существу и означает расширение его до исчисления предикатов), например, следующими "постулатами Бернайса": аксиомами A (t) É $xA (x) и "xA (x) É A (t) и правилами вывода "если доказано С ÉА (х) É С, то можно считать доказанным и С É "хA (х)" и "если доказано А (х) ÉС, то можно считать доказанным и $ хA (x) É " (здесь х не входит свободно в С).   К К общности и существования сводятся и др. виды К, например вместо так называемого К единственности $! x ("существует единственный х такой, что") можно писать "обычные" К, заменяя $! xA (x) на $ xA (x) &"y"z (A (y)&A (z) É y = z). Аналогично, К, "ограниченный" каким-либо одноместным предикатом (x)($x (x), читается как "существует x, удовлетворяющий свойству Р и такой, что", а "xp (x) — "для всех х, удовлетворяющих свойству Р, верно, что"), легко выразить через К общности и существования и операторы импликации и конъюнкции: $xp (x) A (x) º $x ( (x)&A (x)) и "xp (x) A (x) º "x ( (x)ÉA (x)).   Лит.: Клини С. К, Введение в метаматематику, пер. с англ., М., 1957, с. 72—80, 130—138; Черч А., Введение в математическую логику, пер. с англ., т. 1, М., 1960, с. 42—48.   Ю.А. Гастев.