
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Квадратное уравнение | Квадратное уравнение (далее К) уравнение вида ax2 + bx + с = 0, где а, b, с - какие-либо числа, называются коэффициентами уравнения. К имеет два корня, которые находятся по формулам:
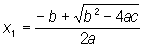
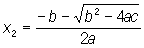
Выражение D = b2 - 4ac называется дискриминантом К Если D > 0, то корни К действительные различные, если D < 0, то корни сопряженные комплексные, если D = 0, то корни действительные равные. Имеют место формулы Виета: x1 +х2 = -b/a, x1x2 = с/а, связывающие корни и коэффициенты К Левую часть К можно представить в виде а (х - х1)(х - x2). Функцию у = ax2 + bx + с называют квадратным трехчленом, ее графиком служит парабола с вершиной в точке М (-b/2a; с - b2/4a) и осью симметрии, параллельной оси Оу; направление ветвей параболы совпадает со знаком a. Решение К было известно в геометрической форме еще математикам древности. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 05.03.2026 00:59:14
|

|

|
 |
|

|
 |
 |
 |
|