
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Кардано формула | Кардано формула (далее К) формула для нахождения корней кубического уравнения
x3 + px + q = 0
(к такому виду может быть приведено всякое кубическое уравнение). К имеет следующий вид:
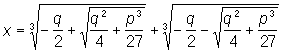
Всякий кубический корень имеет три значения, среди которых не более одного действительного. Значения кубических корней, стоящих в К, следует брать такими, чтобы их произведение было равно —р/3; именно эти значения и нужно складывать, чтобы получить корень уравнения. Таким путем можно найти три корня уравнения (см. Кубическое уравнение). К названа по имени Дж. Кардано и впервые была опубликована им в 1545, хотя вопрос о том, была она найдена самим Кардано или заимствована им от Н. Тартальи, или даже еще раньше (около 1515) открыта С. Ферро, нельзя считать вполне решенным. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 10.03.2026 00:14:08
|

|

|
 |
|

|
 |
 |
 |
|