
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Интегральный логарифм | Интегральный логарифм (далее И) специальная функция, определяемая интегралом
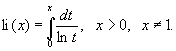
Этот интеграл не выражается в конечной форме через элементарные функции. Если х > 1, то интеграл понимается в смысле главного значения:
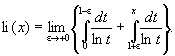
И введен в математический анализ Л. Эйлером в 1768. И li(x) связан с интегральной показательной функцией Ei(x) соотношением li(x) = Ei(lnx). Для больших положительных х функция li(x) растет как x / lnx. И играет важную роль в аналитической теории чисел, так как число простых чисел, не превосходящих х, приблизительно равно li(x).
Лит.: Янке Е., Эмде Ф., Леш Ф., Специальные функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М., 1968. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 22.02.2026 15:04:37
|

|

|
 |
|

|
 |
 |
 |
|