|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Интегральные уравнения | Интегральные уравнения (далее И) уравнения, содержащие неизвестные функции под знаком интеграла. Многочисленные задачи физики и математической физики приводят к И. у. различных типов. Пусть, например, требуется с помощью некоторого оптического прибора получить изображение линейного объекта А, занимающего отрезок 0 £ x £ l оси Ox, причем освещенность объекта характеризуется плотностью u(x). Изображение В представляет собой некоторый отрезок другой оси x1; последний путем подходящего выбора начала отсчета и единицы длины также можно совместить с отрезком 0 £ x1 £ l . Если дифференциально малый участок (х, х + Dх) объекта А вызывает освещенность изображения В с плотностью (x1, x)u(x)dx, где функция (x1, x) определяется свойствами оптического прибора, то полная освещенность изображения будет иметь плотность
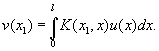
В зависимости от того, хотят ли добиться заданной освещенности v(x1) изображения или "точного" фотографического изображения (v(x) = ku(x), где постоянная k заранее не фиксируется), или, наконец, определенной разницы освещенности А и В (u(x) - v(x) = f(x)), приходят к различным И относительно функции u(x):
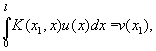
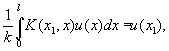
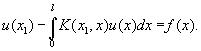
Вообще, линейным интегральным уравнением 1-го рода называется уравнение вида
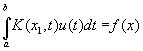
линейным интегральным уравнением 2-го рода, или уравнением Фредгольма,-уравнение вида
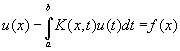
(при f (x) º 0 оно называется однородным уравнением Фредгольма); обычно рассматриваются уравнения Фредгольма с параметром l:
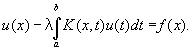
Во всех уравнениях функция
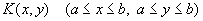
- так называемое ядро И - известна, так же, как функция f (x) (а £ х £ b); искомой является функция u(x) (а £ х £ b).
Функции (x, y), f (x), u(x) и параметр уравнения l могут принимать как действительные, так и комплексные значения. В частном случае, когда ядро (x, y) обращается в нуль при у > х, получается уравнение Вольтерра:
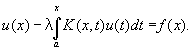
И называется особым, если хотя бы один из пределов интегрирования бесконечен или ядро (x, y) обращается в бесконечность в одной или нескольких точках квадрата а £ х £ b, а £ y £ b или на некоторой линии. И может относиться и к функциям нескольких переменных: таково, например, уравнение
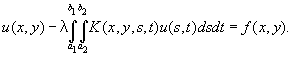
Рассматриваются также нелинейные И, например уравнения вида
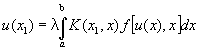
или
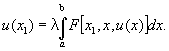
Линейные И 2-го рода решаются следующими методами: 1) решение u(x) получается в виде ряда по степеням l (сходящегося в некотором круге |l|<) с коэффициентами, зависящими от х (метод Вольтерра - Неймана); 2) решение u(x), при тех значениях l, при которых оно вообще существует, выражается через некоторые целые функции от l (метод Фредгольма); 3) в случае, когда ядро симметрично, т. е. К(х, y) º К(у, x), решение u(x) выражается в виде ряда по ортогональным функциям uк(х), являющимся ненулевыми решениями соответствующего однородного уравнения
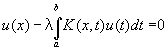
(последнее имеет отличные от нуля решения лишь при некоторых специальных значениях параметра l = lк, k = 1, 2, ...) (метод Гильберта - Шмидта); 4) в некоторых частных случаях решение сравнительно просто получается с помощью Лапласа преобразования; 5) в случае, когда
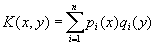
(так называемое вырожденное ядро), отыскание u(х) сводится к решению системы алгебраических уравнений. Приближенные решения можно получить, либо применив к 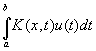 какую-либо формулу численного интегрирования, либо заменив данное ядро К(х, y) некоторым вырожденным ядром, мало отличающимся от К(х, у). К И часто сводятся краевые задачи для дифференциальных уравнений, обыкновенных и с частными производными; такое сведение имеет и теоретическую и практическую ценность.
Лит.: Смирнов В. И., Курс высшей математики, 3 изд., т. 4, М., 1957; Петровский И. Г., Лекции по теории интегральных уравнений, 3 изд., М., 1965; Канторович Л. В. и Крылов В. И., Приближенные методы высшего анализа, 5 изд., Л. - М., 1962.
Д. А. Васильков. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 14:22:32
|
|
|
|
|
|
|
|
|
|
|
