
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Аналитические функции | Аналитические функции (далее А) функции, которые могут быть представлены степенными рядами. Исключительная важность класса А определяется следующим. Во-первых, этот класс достаточно широк; он охватывает большинство функций, встречающихся в основных вопросах математики и ее приложений к естествознанию и технике. Аналитическими являются элементарные функции — многочлены, рациональные функции, показательная и логарифмическая, степенная, тригонометрические и обратные тригонометрические, гиперболические и им обратные, алгебраические функции, и специальные функции — эллиптические, цилиндрические и др. Во-вторых, класс А замкнут относительно основных операций арифметики, алгебры и анализа; применение арифметических действий к функциям этого класса, решение алгебраических уравнений с аналитическими коэффициентами, дифференцирование и интегрирование А приводят снова к А Наконец, А обладают важным свойством единственности; каждая А образует одно "органически связанное целое", представляет собой "единую" функцию во всей своей естественной области существования. Это свойство, которое в 18 в. считалось неотделимым от самого понятия функции, приобрело принципиальное значение после установления в 1-й половине 19 в. общей точки зрения на функцию как на произвольное соответствие.
Теория А создана в 19 в., в первую очередь благодаря работам О. Коши, Б. Римана и К. Вейерштрасса. Решающую роль в построении этой теории сыграл "выход в комплексную область" — переход от действительного переменного х к комплексному переменному z = х + iy, которое может меняться в произвольной области комплексной плоскости. Теория А возникла как теория функций комплексного переменного; в некотором смысле именно аналитические (а не произвольные комплексные функции двух действительных переменных х и y) естественно считать функциями комплексного переменного z. Теория А составляет основное содержание общей теории функций комплексного переменного. Поэтому часто под теорией функций комплексного переменного понимают именно теорию А
Существуют различные подходы к понятию аналитичности. В основе одного из них, впервые развитого Коши и далеко продвинутого Риманом, лежит структурное свойство функции — существование производной по комплексному переменному, или комплексная дифференцируемость. Этот подход тесно связан с геометрическими соображениям и. Другой подход, систематически развивавшийся Вейерштрассом, основывается на возможности представления функций степенными рядами; он связан, тем самым, с аналитическим аппаратом, которым может быть изображена функция. Основной факт теории А заключается в тождественности соответствующих классов функций, рассматриваемых в произвольной области комплексной плоскости.
Приведем точные определения. Всюду в дальнейшем через z обозначается комплексное число х + iy, где x и y — действительные числа. Геометрически число z изображается точкой плоскости с координатами х и y; евклидова плоскость, точки которой отождествляются с комплексными числами, называется комплексной плоскостью. Пусть D — область (открытое связное множество) в комплексной плоскости. Если каждой точке z области D приведено в соответствие некоторое комплексное число w, то говорят, что в области D определена (однозначная) функция f комплексного переменного z, и пишут: w = f(z), z(D. Функция w = f(z) = f(x + iy) комплексного переменного z (D может рассматриваться как комплексная функция двух действительных переменных х и y, определенная в области D. Полагая w = u + iv, где u и v — действительные числа, замечают, что задание такой функции f эквивалентно заданию двух действительных функций j и y двух действительных переменных х и y, определенных в той же области:
u = j(x, y), v = y(x, y), (x, y)ÎD.
Пусть z — фиксированная точка области D. Придадим z произвольное приращение Dz = Dx + iDy (так, чтобы точка z+Dz оставалась в пределах области D) и рассмотрим соответствующее приращение функции f : Df (z) = f (z + (z) — f (z). Если разностное отношение Df (z)/Dz имеет предел при Dz®0, т. е. существует комплексное число А такое, что для любого e > 0 будет ïDf(z)/Dz - Aï < e как только ïDzï < d (d = d(e) > 0), то функция f называется моногенной в точке z, а число А — ее производной в этой точке: А = f" (z) = df(z)/dz. Функция, моногенная в каждой точке области D, называется моногенной в области D.
Если функция f моногенна в точке zÎD, то f и соответствующие функции j и y имеют в этой точке частные производные по х и y; при этом ¶f/¶x = ¶y/¶x + i(¶y/¶x), ¶f/¶y = ¶j/¶y + i(¶y/¶y). Производную f` (z ) можно выразить через частные производные f по х и по у (достаточно вычислить предел отношения Df(z)/Dz двумя разными способами — при Dz = Dx ® 0 и при Dz = iDy ® 0; приравнивая соответствующие выражения, получаем ¶f/¶x = (1/i)¶f/¶y или, что то же самое, ¶f/¶x + i(¶f/¶y) = 0. Переходя к функциям j и y, это равенство можно переписать так: ¶j/¶x = ¶y/¶y, ¶j/¶y = — ¶y/¶x. Если функция f моногенна в области D, то последние соотношения справедливы в каждой точке области D; они называются уравнениями Коши — Римана. Следует отметить, что эти уравнения встречались уже в 18 в. в связи с изучением функций комплексного переменного в трудах Д"Аламбера и Л. Эйлера.
Моногенность функции f эквивалентна ее дифференцируемости в смысле комплексного анализа. При этом под дифференцируемостыо f в точке zÎD понимается возможность представления ее приращения в виде Df(z) =ADz + a(Dz)Dz, где a(Dz) ® 0 при Dz ® 0; дифференциал df(z) функции f в точке z, равный главной части ADz ее приращения Df(z), в этом случае пропорционален dz = Dz и имеет вид f`(z) dz. Полезно сравнить понятия дифференцируемости функции f — в смысле действительного анализа и в смысле комплексного анализа. В первом случае дифференциал df имеет вид (¶f/¶x) dx + (¶f/¶y) dy. Удобно переписать это выражение в комплексной форме. Для этого переходят от независимых переменных x, у к переменным z,  , которые формально можно считать новыми независимыми переменными, связанными со старыми соотношениями: z = х + iy, , которые формально можно считать новыми независимыми переменными, связанными со старыми соотношениями: z = х + iy, 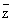 = x - iy (становясь на эту точку зрения, функцию f иногда записывают в виде f(z, = x - iy (становясь на эту точку зрения, функцию f иногда записывают в виде f(z, 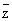 ). Выражая dx и dy через dz и d ). Выражая dx и dy через dz и d 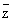 по обычным правилам вычисления дифференциалов, получают df = (¶f/¶z)dz + (¶f/¶ по обычным правилам вычисления дифференциалов, получают df = (¶f/¶z)dz + (¶f/¶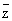 )d )d 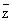 , где ¶f/¶z = (1/2) (¶f/¶x - i¶f/¶y) и ¶f/¶ , где ¶f/¶z = (1/2) (¶f/¶x - i¶f/¶y) и ¶f/¶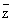 = (1/2) (¶f/¶x + i¶f/¶y) (формальные) производные функции f по z и = (1/2) (¶f/¶x + i¶f/¶y) (формальные) производные функции f по z и 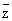 соответственно. соответственно.
Отсюда уже нетрудно заключить, что дифференцируемость функции f в смысле комплексного анализа имеет место в том и только том случае, когда она дифференцируема в смысле действительного анализа и справедливо равенство ¶f/¶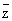 = 0, являющееся краткой формой записи уравнений Коши — Римана; при этом = 0, являющееся краткой формой записи уравнений Коши — Римана; при этом
¶f/¶z = f` = df/dz.
Равенство ¶f/¶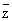 = 0 показывает, что дифференцируемыми в смысле комплексного анализа являются те и только те функции f, которые, рассматриваемые формально как функции независимых переменных z и = 0 показывает, что дифференцируемыми в смысле комплексного анализа являются те и только те функции f, которые, рассматриваемые формально как функции независимых переменных z и 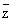 "зависят только от z", являются "функциями комплексного переменного z". "зависят только от z", являются "функциями комплексного переменного z".
Интеграл от функции f = j + iy вдоль (ориентированной спрямляемой) кривой Г можно определить с помощью понятия криволинейного интеграла:

Центральное место в теории моногенных функций (теории Коши) занимает следующая итегральная теорема Коши: если функция моногенна в односвязной области D, то Г f(z)dz = 0 для любой замкнутой кривой Г, лежащей в этой области. В произвольной области D то же утверждение справедливо для замкнутых кривых Г, которые непрерывной деформацией могут быть стянуты в точку (оставаясь в пределах области D). Опираясь на интегральную теорему Коши, нетрудно доказать интегральную формулу Коши: если функция f моногенна в области D и Г — простая замкнутая кривая, принадлежащая области D вместе со своей внутренностью DГ то для любой точки zÎDГ
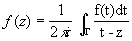
(ориентация кривой Г предполагается положительной относительно области D Г)
Пусть функция f моногенна в области D. Фиксируем произвольную точку z0 области D и обозначим через g окружность с центром в точке z0 и радиусом r > 0, принадлежащую, вместе со всем кругом: К: Iz - z0 < r, области D. Тогда
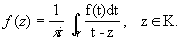
Представим ядро Коши 1/(t—z) для tÎg и zÎ в виде суммы бесконечной геометрической прогрессии:
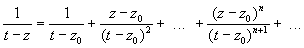
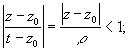
поэтому ряд сходится равномерно относительно tÎg при любом фиксированном zÎ, интегрируя этот ряд — после умножения на
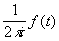
— почленно, получают разложение функции f в степенной ряд
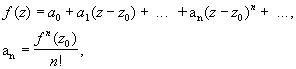
сходящийся в круге : z - z0 < r.
Уточним теперь понятие аналитичности. Пусть f — функция, определенная в области D; она называется аналитической (или голоморфной) в точке z0 области , если существует окрестность этой точки (круг с центром в z0), в которой функция f представляется степенным рядом:
f (z) = a0 + a1(z - z0) + a2(z - z0)2 +. . . . + an(z - z0)n+ . . .
Если это свойство имеет место в каждой точке z0 области D, то функция f называется аналитической (голоморфной) в области D.
Выше было показано, что функция f, моногенная в области D, аналитична в этой области. В отдельной точке это утверждение неверно; например, функция f(z) = êzê2 = z моногенна в точке z0 = 0, но нигде не аналитична. С другой стороны, функция f , аналитическая в точке z0 области D, моногенна в этой точке. Более того, сумма сходящегося степенного ряда имеет производные всех порядков (бесконечно дифференцируема) по комплексному переменному z; коэффициенты ряда могут быть выражены через производные функции f в точке z0 по формулам: an=f(n)(z0)/n!. Степенной ряд, записанный в форме моногенна в точке z0 = 0, но нигде не аналитична. С другой стороны, функция f , аналитическая в точке z0 области D, моногенна в этой точке. Более того, сумма сходящегося степенного ряда имеет производные всех порядков (бесконечно дифференцируема) по комплексному переменному z; коэффициенты ряда могут быть выражены через производные функции f в точке z0 по формулам: an=f(n)(z0)/n!. Степенной ряд, записанный в форме
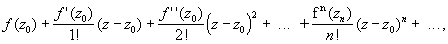
называется рядом Тейлора функции f в точке z0. Тем самым, аналитичность функции f в области D означает, что в каждой точке области D функция f бесконечно дифференцируема и ее ряд Тейлора сходится к ней в некоторой окрестности этой точки.
Следовательно, понятия моногенности и аналитичности функции в области тождественны и каждое из следующих свойств функции f в области D — моногенность, дифференцируемость в смысле комплексного анализа, дифференцируемость в смысле действительного анализа вместе с выполнением уравнений Коши — Римана — может служить определением аналитичности f в этой области.
Важнейшее свойство А выражается следующей теоремой единственности: две функции, аналитические в области D и совпадающие на каком-либо множестве, имеющем предельную точку в D, совпадают и во всей области D (тождественны). В частности, аналитическая в области функция, отличная от тождественного нуля, может иметь в области лишь изолированные нули.
Если Е — произвольное множество (в комплексной плоскости и, в частности, на действительной прямой), то функция f (z), zÎE, называется аналитической на множестве E, если каждая точка этого множества имеет окрестность, на пересечении которой с множеством Е функция f представляется сходящимся степенным рядом; это означает в действительности, что f аналитична на некотором открытом множестве, содержащем Е (точнее, существует открытое множество, содержащее Е, и аналитическая на нем функция, f совпадающая с f на множестве E). Для открытых множеств понятие аналитичности совпадает с понятием дифференцируемости по множеству (моногенности). Однако в общем случае это не так; в частности, на действительной прямой существуют функции, не только имеющие производную, но и бесконечно дифференцируемые в каждой точке, которые не являются аналитическими ни в одной точке этой прямой. Например,
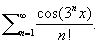
С другой стороны, для справедливости теоремы единственности А существенно свойство связности множества E. Поэтому А рассматриваются обычно в областях, т.е. на открытых и связных множествах.
Важную роль в изучении А играют точки, в которых нарушается свойство аналитичности — т. н. особые точки А Рассмотрим здесь изолированные особые точки (однозначных) А Пусть f — А в области вида 0 < |z - z0| < r; в этой области f разлагается в ряд Лорана:
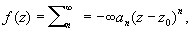
содержащий, вообще говоря, не только положительные, но и отрицательные степени z - z0. Если в этом разложении члены с отрицательными степенями отсутствуют (an = 0 для n = -1, -2,...), то z0 называется правильной точкой f. В правильной точке существует и конечен
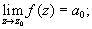
полагая f(z0) = a0, получают функцию, аналитическую во всем круге ïz - z0ï < r.
Если ряд Лорана функции f содержит лишь конечное число членов с отрицательными степенями z - z0:
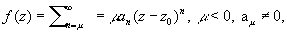
то точка z0 называется полюсом функции f (порядка m); полюс z0 характеризуется тем, что
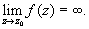
В случае, если ряд Лорана содержит бесконечное число отрицательных степеней z — z0, то z0 называется существенно особой точкой; в таких точках не существует ни конечного, ни бесконечного предела функции f. Если z0 — изолированная особая точка функции f, то коэффициент a-1 в ее разложении в ряд Лорана называется вычетом функции f в точке z0.
Функции, представимые в виде отношения двух функций, аналитических в области D, называется мероморфными в области D. Мероморфная в области функция аналитична в этой области за исключением, быть может, конечного или счетного множества полюсов; в полюсах значения мероморфной функции считаются равными бесконечности. Если допустить такие значения, то мероморфные в области D функции могут быть определены как функции, которые в окрестности каждой точки z0 области D представимы рядом по степеням z — z0, содержащим конечное (зависящее от z0) число членов с отрицательными степенями z — z0.
Часто аналитическими в области D называют как аналитические (голоморфные), так и мероморфные в этой области функции. В этом случае голоморфные функции называют также регулярными аналитическими или просто регулярными. Простейший класс А составляют функции, аналитические во всей плоскости; такие функции называют целыми. Целые функции представляются рядами вида
a0 + a1z + a2z2 + ... + anzn +...,
сходящимися во всей комплексной плоскости. К ним относятся многочлены от z, функции
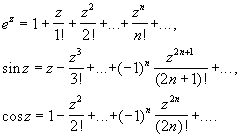
Функции, мероморфные во всей плоскости (т. е. представимые в виде отношения целых функций), называются мероморфными функциями. Таковыми являются рациональные функции от z (отношения многочленов),
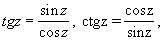
эллиптические функции и т. д.
Для изучения А важное значение имеют связанные с ними геометрические представления. Функцию w = f(z), z(D можно рассматривать как отображение области D в плоскость переменного w. Если f есть А, то образ f(D) области D также является областью (принцип сохранения области). Из условия комплексной дифференцируемости функции f в точке z0ÎD следует, что при f`(z0) ¹ 0 соответствующее отображение сохраняет углы в z0, как по абсолютному значению, так и по знаку, т. е. является конформным. Т.о., существует тесная связь между аналитичностью и важным геометрическим понятием конформного отображения. Если f аналитична в D и f(z¢) ¹ f(z¢¢) при z¢ ¹ z¢¢ (такие функции называются однолистными), то f¢ (z) ¹ 0 в D и f определяет взаимно однозначное и конформное отображение области D на область G = f(D). Теорема Римана — основная теорема теории конформных отображений — утверждает, что в любой односвязной области, граница которой содержит более одной точки, существуют однолистные А, конформно отображающие эту область на круг или полуплоскость.
Дифференцируя уравнения Коши — Римана, нетрудно усмотреть, что действительная и мнимая части функции f = j+iy, аналитичны в области D, удовлетворяют в этой области уравнению Лапласа:
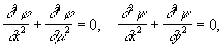
т. е. являются гармоническими функциями. Две гармонические функции, связанные между собой уравнениями Коши — Римана, называются сопряженными. В односвязной области D любая гармоническая функция j имеет сопряженную функцию y и является, тем самым, действительной частью некоторой аналитической в D функции f. Связи с конформными отображениями и гармоническими функциями лежат в основе многих приложений теории А
Все сказанное выше относилось к однозначным А f рассматриваемым в данной области D комплексной плоскости. Задаваясь вопросом о возможности продолжения функции f как А в большую область, приходят к понятию А, рассматриваемой в целом — во всей своей естественной области существования. При таком продолжении данной функции область ее аналитичности, расширяясь, может налегать сама на себя, доставляя новые значения функции в точках плоскости, где она уже была определена. Поэтому А, рассматриваемая в целом, вообще говоря, оказывается многозначной. К необходимости изучения многозначных А приводят многие вопросы теории функций (обращение функций, нахождение первообразных и построение А с заданной действительной частью — в многосвязных областях, решение алгебраических уравнений с аналитичными коэффициентами и др.); такими функциями являются
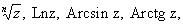
алгебраические функции и т. д. Регулярный процесс, приводящий к полной А, рассматриваемой в своей естественной области существования, был указан К. Вейерштрассом; он носит название аналитического продолжения по Вейерштрассу.
Исходным является понятие элемента А — степенного ряда с ненулевым радиусом сходимости. Такой элемент 0: a0 + a1(z - z0) + a2(z - z0)2 + ... + an(z - z0)n + ... определяет некоторую А f в своем круге сходимости 0. Пусть z1 — точка круга 0, отличная от z0. Разлагая функцию f в ряд Тейлора с центром в точке z1, получают новый элемент 1:
b0 + b1(z - z1) + b2(z- z1)2 + ... +bn (z— z1)n + ... ,
круг сходимости которого обозначают через 1. В общей части кругов 0 и 1 ряд 1 сходится к той же функции, что и ряд 0. Если круг 1 выходит за пределы круга 0, то ряд 1 определяет функцию, заданную посредством 0, на некотором множестве вне 0 (где ряд 0 расходится). В этом случае элемент 1 называется непосредственным аналитичным продолжением элемента 0. Пусть 0, 1 ..., — цепочка элементов такая, что i+1 является непосредственным аналитичным продолжением i (i = 1, ..., — 1); тогда элемент называется аналитичным продолжением элемента 0 (посредством данной цепочки элементов). Может оказаться так, что центр круга принадлежит кругу 0, но элемент не является непосредственным аналитичным продолжением элемента 0. В этом случае суммы рядов 0 и в общей части кругов 0 и имеют различные значения; тем самым аналитичное продолжение может привести к новым значениям функции в круге 0.
Совокупность всех элементов, которые могут быть получены аналитичным продолжением элемента 0, образует полную А (в смысле Вейерштрасса), порожденную элементом 0; объединение их кругов сходимости представляет собой (вейерштрассову) область существования этой функции. Из теоремы единственности А следует, что А в смысле Вейерштрасса полностью определяется заданием элемента 0 При этом в качестве исходного может быть взят любой др. элемент, принадлежащий этой функции; полная А от этого не изменится.
Полная А f, рассматриваемая как функция точек плоскости, принадлежащих ее области существования D, вообще говоря, является многозначной. Чтобы избавиться от многозначности, функцию f рассматривают не как функцию точек плоской области D, а как функцию точек некоторой (лежащей над областью D) многолистной поверхности R такой, что каждой точке области D соответствует столько (проектирующихся в нее) точек поверхности R, сколько различных значений принимает функция f в этой точке: на поверхности R функция f становится однозначной функцией. Идея перехода к таким поверхностям принадлежит Б. Риману, а сами они называются римановы поверхности. Схематическое изображение римановых поверхностей функций 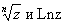 приведены на рис. 1 и 2 (соответственно). Абстрактное определение понятия римановой поверхности позволило заменить теорию многозначных А теорией однозначных А на римановых поверхностях. приведены на рис. 1 и 2 (соответственно). Абстрактное определение понятия римановой поверхности позволило заменить теорию многозначных А теорией однозначных А на римановых поверхностях.
Фиксируем область D, принадлежащую области существования D полной А f, и какой-либо элемент функции f с центром в точке области D. Совокупность всех элементов, которые могут быть получены аналитичным продолжением элемента посредством цепочек, центры которых принадлежат D, называется ветвью А f . Ветвь многозначной А может оказаться однозначной А в области D. Так, например, произвольные ветви функций 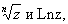 соответствующие любой односвязной области, не содержащей точку , являются однозначными функциями; при этом соответствующие любой односвязной области, не содержащей точку , являются однозначными функциями; при этом 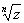 имеет ровно n, a Lnz — бесконечное множество различных ветвей в каждой такой области. Выделение однозначных ветвей (с помощью тех или иных разрезов области существования) и их изучение средствами теории однозначных А являются одним из основных приемов исследования конкретных многозначных А имеет ровно n, a Lnz — бесконечное множество различных ветвей в каждой такой области. Выделение однозначных ветвей (с помощью тех или иных разрезов области существования) и их изучение средствами теории однозначных А являются одним из основных приемов исследования конкретных многозначных А
Понятие А нескольких переменных вводится с помощью кратных степенных рядов — совершенно аналогично тому, как это было сделано выше для А одного переменного. А нескольких комплексных переменных по своим свойствам также во многом аналогичны А одного комплексного переменного; однако они обладают и рядом принципиально новых свойств, не имеющих аналогов в теории А одного переменного. Более общим является понятие А на комплексных многообразиях (понятие комплексного многообразия является обобщением понятия римановой поверхности для многомерного случая).
Лит.: Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; Смирнов В. И., Курс высшей математики, 8 изд., т. 3, ч. 2, М.—Л., 1969; Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1—2, М., 1967—68; Лаврентьев М. А., Шабат Б. В., Методы теории функций комплексного переменного, 3 изд., М., 1965; Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; Евграфов М. А., А, 2 изд., М., 1968; Свешников А. Г., Тихонов А. Н., Теория функций комплексной переменной, М., 1967; Фукс Б. А., Теория аналитических функций многих комплексных переменных, 2 изд., М., 1963; Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; Маркушевич А. И., Очерки по истории теории аналитических функций, М.— Л., 1951; Математика в СССР за тридцать лет, 1917 — 1947, М.— Л., 1948, с. 319—414; Математика в СССР за сорок лет, 1917 — 1957, т. 1, М., 1959, с. 381—510.
А. А. Гончар.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:42:59
|

|

|
 |
|

|
 |
 |
 |
|