|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Инварианты | Инварианты (далее И) (от лат. invarians, родительный падеж invariantis - неизменяющийся), числа, алгебраические выражения и т. п., связанные с каким-либо математическим объектом и остающиеся неизменными при определенных преобразованиях этого объекта или системы отсчета, в которой описывается объект. Чтобы охарактеризовать какую-либо геометрическую фигуру и ее положение с помощью чисел, обычно приходится вводить некоторую вспомогательную систему отсчета или систему координат. Полученные в такой системе числа x1, x2,..., xn характеризуют не только изучаемую геометрическую фигуру, но и ее отношение к системе отсчета, и при изменении этой системы фигуре будут отвечать другие числа x¢1, х¢2,..., х¢n. Поэтому если значение какого-либо выражения f (x1, x2,..., xn) характерно для фигуры самой по себе, то оно не должно зависеть от системы отсчета, т. е. должно выполняться соотношение
f (x1, x2,..., xn) = f (x¢1, x¢2,..., x¢n). (1)
Все выражения, удовлетворяющие соотношению (1), называются инвариантами. Например, положение отрезка M1M2 на плоскости определяется в прямоугольной системе координат двумя парами чисел x1, y1 и x2, y2 - координатами его концов M1 и M2. При преобразовании координатной системы (путем смещения ее начала и поворота осей) точки M1 и M2 получают другие координаты x¢1, у¢1 и x¢2, у¢2, однако (x1 - x2)2 + (y1 - y2)2 = (x¢1 - x¢2)2 + (y¢1 - у¢2)2. Поэтому выражение (x1 - x2)2 + (y1 - - y2)2 является И преобразования прямоугольных координат. Геометрический смысл этого И ясен: это квадрат длины отрезка M1M2.
Кривая 2-го порядка в прямоугольной системе координат задается уравнением 2-й степени
ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0, (2)
коэффициенты которого можно рассматривать как числа, определяющие кривую. При преобразовании прямоугольных координат эти коэффициенты изменяются, но выражение 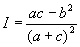 сохраняет свое значение и, следовательно, служит И кривой (2). При рассмотрении кривых и поверхностей высших порядков возникает аналогичная более общая задача.
Понятие И употреблялось еще немецким математиком О. Гессе (1844), но систематическое развитие теория И получила у английского математика Дж. Сильвестра (1851-52), предложившего и термин "И". В течение 2-й половины 19 в. теория И была одной из наиболее разрабатываемых математических теорий. В процессе развития этой классической теории И главные усилия исследователей стали постепенно сосредоточиваться вокруг решения нескольких "основных" проблем, наиболее известная из которых формулировалась следующим образом. Рассматриваются И системы форм, являющиеся целыми рациональными функциями от коэффициентов этих форм. Требуется доказать, что для И каждой конечной системы форм существует конечный базис, т. е. конечная система целых рациональных И, через которые каждый другой целый рациональный И выражается в виде целой рациональной функции. Это доказательство для проективных И было дано в конце 19 в. немецким математиком Д. Гильбертом.
Весьма плодотворный подход к понятию И получается, если системы чисел x1, x2,..., xn и x¢1, х¢2,..., х¢n рассматривать не как координаты одной и той же точки относительно различных координатных систем, а как координаты различных точек в одной и той же системе координат, полученных одна из другой движением. Движения пространства образуют группу. И относительно изменений систем координат являются также И относительно группы движений. Отсюда путем непосредственного обобщения получается понятие И любой группы преобразований. Теория таких И оказывается весьма тесно связанной с теорией групп и в особенности с теорией представлений групп.
Понятие И группы преобразований лежит в основе известной систематизации геометрических дисциплин по группам преобразований, И которых изучаются в этих дисциплинах. Например, И группы ортогональных преобразований изучаются в обычной евклидовой геометрии, И аффинных преобразований - в аффинной, И проективных - в проективной. Весьма общую группу преобразований составляют все взаимно однозначные и непрерывные преобразования. Изучение И этих так называемых топологических преобразований составляет предмет топологии. В дифференциальной геометрии основное значение имеют дифференциальные И, развитие теории которых привело к созданию тензорного исчисления.
В 20 в. глубокое влияние на развитие теории И, в частности на развитие тензорного исчисления, оказала теория относительности, в которой инвариантность физических законов относительно группы движений становится одним из руководящих принципов. См. также Инвариантность.
Лит.: Погорелов А. В.. Аналитическая геометрия, 3 изд., М., 1968; Широков П. А., Тензорный анализ, ч. 1, М.-Л., 1934; Гуревич Г. Б., Основы теории алгебраических инвариантов, М.-Л., 1948; Вейль Г., Классические группы, их инварианты и представления, пер. с англ., М., 1947. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 06.11.2024 03:13:43
|
|
|
|
|
|
|
|
|
|
|
