|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Изоморфизм (матем.) | Изоморфизм (далее И) одно из основных понятий современной математики, возникшее сначала в пределах алгебры в применении к таким алгебраическим образованиям, как группы, кольца, поля и т. п., но оказавшееся весьма существенным для общего понимания строения и области возможных применений каждого раздела математики.
Понятие И (матем.) относится к системам объектов с заданными в них операциями или отношениями. В качестве простого примера двух изоморфных систем можно рассмотреть систему R всех действительных чисел с заданной на ней операцией сложения x = x1+ x1 и систему Р положительных действительных чисел с заданной на ней операцией умножения y = y1y2. Можно показать, что внутреннее "устройство" этих двух систем чисел совершенно одинаково. Для этого достаточно систему R отобразить в систему Р, поставив в соответствие числу х из R число у = ax (а > 1) из Р. Тогда сумме x = x1 + x2 будет соответствовать произведение y = y1y2 чисел 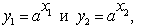 соответствующих x1 и x2. Обратное отображение Р на R имеет при этом вид x = loga y. Из любого предложения, относящегося к сложению чисел системы R, можно извлечь соответствующее ему предложение, относящееся к умножению чисел системы Р. Например, если в R сумма
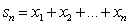
членов арифметической прогрессии выражается формулой
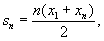
то в Р произведение
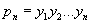
членов геометрической прогрессии выражается формулой
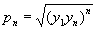
(умножению на n в системе R соответствует при переходе к системе Р возведение в n-ю степень, а делению на два - извлечение квадратного корня).
Изучение свойств одной из изоморфных систем в значительной мере (а с абстрактно-математической точки зрения - полностью) сводится к изучению свойств другой. Любую систему объектов ", изоморфную системе , можно рассматривать как "модель" системы ("моделировать систему при помощи системы " ") и сводить изучение самых разнообразных свойств системы к изучению свойств "модели" ".
Общее определение И (матем.) систем объектов с заданными на них в конечном числе отношениями между постоянным для каждого отношения числом объектов таково. Пусть даны две системы объектов и ", причем в первой определены отношения
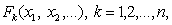
а во второй - отношения
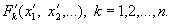
Системы и " с указанными в них отношениями называются изоморфными, если их можно поставить в такое взаимно однозначное соответствие
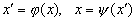
(где х - произвольный элемент , а x" - произвольный элемент "), что из наличия k (x1,x2,...) вытекает "k (х"1,х"2,...), и наоборот. Само указанное соответствие называется при этом изоморфным отображением, или изоморфизмом. (В приведенном выше примере в системе R определено отношение (x, x1, x2), где x = x1 + x2, в системе Р - отношение " (y, y1, y2), где у = у1у2; взаимно однозначное соответствие устанавливается по формулам у = ax, х = 1ogay.)
Понятие И (матем.) возникло в теории групп, где впервые был понят тот факт, что изучение внутренней структуры двух изоморфных систем объектов представляет собой одну и ту же задачу.
Аксиомы любой математической теории определяют систему объектов, изучаемую этой теорией, всегда только с точностью до И (матем.): аксиоматически построенная математическая теория, применимая к какой-либо одной системе объектов, всегда полностью применима и к другой. Поэтому каждая аксиоматически изложенная математическая теория допускает не одну, а много "интерпретаций", или "моделей" (см., например, в ст. Геометрия, раздел Истолкование геометрии).
Понятие И (матем.) включает в себя как частный случай понятие гомеоморфизма, играющее основную роль в топологии.
Частным случаем И (матем.) является автоморфизм - взаимно однозначное отображение
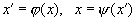
системы объектов с заданными отношениями k(x1, x2, ...) на самое себя, при котором из k(x1, x2, ...) вытекает "k(x"1, x"2, ...), и наоборот. Это понятие тоже возникло в теории групп, но потом оказалось существенным в самых различных разделах математики.
Лит.: Курош А. Г., Курс высшей алгебры, 3 изд., М. - Л., 1952; Энциклопедия элементарной математики, под ред. П. С. Александрова (и др.), кн. 2, М. - Л., 1951. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 31.10.2025 13:57:47
|
|
|
|
|
|
|
|
|
|
|
