
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Изображение оптическое | Изображение оптическое (далее И) картина, получаемая в результате действия оптической системы на лучи, испускаемые объектом, и воспроизводящая контуры и детали объекта. Практическое использование И часто связано с изменением масштаба изображений предметов и их проектированием на поверхность (киноэкран, фотопленку, фотокатод и т. д.). Основой зрительного восприятия предмета является его И, спроектированное на сетчатку глаза.
Максимальное соответствие изображения объекту достигается, когда каждая его точка изображается точкой. Иными словами, после всех преломлений и отражений в оптической системе лучи, испущенные светящейся точкой, должны пересечься в одной точке. Однако это возможно не при любом расположении объекта относительно системы. В случае, например, систем, обладающих осью симметрии (оптической осью), можно получить точечные И лишь тех точек, которые находятся на небольшом угловом удалении от оси, в так называемой параксиальной области. Применение законов геометрической оптики позволяет определить положение И любой точки из параксиальной области; для этого достаточно знать, где расположены кардинальные точки системы.
Совокупность точек, И которых можно получить с помощью оптической системы, образует пространство объектов, а совокупность точечных изображений этих точек - пространство изображений.
И разделяют на действительные и мнимые. Первые создаются сходящимися пучками лучей в точках их пересечения. Поместив в плоскости пересечения лучей экран или фотопленку, можно наблюдать на них действительное И В других случаях лучи, выходящие из оптической системы, расходятся, но если их мысленно продолжить в противоположную сторону, они пересекутся в одной точке. Эту точку называют мнимым изображением точки-объекта; она не соответствует пересечению реальных лучей, поэтому мнимое И невозможно получить на экране или зафиксировать на фотопленке. Однако мнимое И способно играть роль объекта по отношению к другой оптической системе (например, глазу или собирающей линзе), которая преобразует его в действительное.
Оптический объект представляет собой совокупность светящихся собственным или отраженным светом точек. Зная, как оптическая система изображает каждую точку, легко построить и изображение объекта в целом.
И действительных объектов в плоских зеркалах - всегда мнимые (рис. а); в вогнутых зеркалах и собирающих линзах они могут быть как действительными, так и мнимыми в зависимости от удаления объектов от зеркала или линзы (рис. б, г). Выпуклые зеркала и рассеивающие линзы дают только мнимые И действительных объектов (рис. б, д). Положение и размеры И зависят от характеристик оптической системы и расстояния между нею и объектом (см. Увеличение оптическое). Лишь в случае плоского зеркала И по величине всегда равно объекту.
Если точка-объект находится не в параксиальной области, то исходящие из нее и прошедшие через оптическую систему лучи не собираются в одну точку, а пересекают плоскость изображения в разных точках, образуя аберрационное пятно (см. Аберрации оптических систем); размеры этого пятна зависят от положения точки-объекта и конструкции системы. Безаберрационными (идеальными) оптическими системами, дающими точечное изображение точки, являются только плоские зеркала. При конструировании оптических систем аберрации исправляют, т. е. добиваются, чтобы аберрационные пятна рассеяния не ухудшали в заметной степени картины изображения; однако полное уничтожение аберраций невозможно.
Следует отметить, что сказанное выше строго справедливо лишь в рамках геометрической оптики, которая является хотя и достаточно удовлетворительным во многих случаях, но все-таки лишь приближенным способом описания явлений, происходящих в оптических системах. Только в геометрической оптике, где отвлекаются от волновой природы света и, в частности, не учитывают явления дифракции света, И светящейся точки можно считать точечным. Более детальное рассмотрение микроструктуры И, принимающее во внимание волновую природу света, показывает, что изображение точки даже в идеальной (безаберрационной) системе представляет собой не точку, а сложную дифракционную картину (подробнее об этом см. в ст. Разрешающая способность оптических приборов).
Для оценки качества И, получившей большое значение в связи с развитием фотографических, телевизионных и пр. методов, существенно распределение плотности световой энергии в изображении. С этой целью используют особую характеристику - контраст 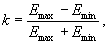 где Emin и Emax - наименьшее и наибольшее значения освещенности в И стандартного тест-объекта; за такой объект обычно принимают решетку, яркость которой меняется по синусоидальному закону с частотой R (число периодов решетки на мм). К зависит от R и направления штрихов решетки. Функция k(R) называется частотно-контрастной характеристикой. В идеальных системах k равен нулю при К = 2А" /lи более, где A" - числовая апертура системы в пространстве изображений, l - длина волны света. Чем меньше k при заданной R, тем хуже качество И в данной системе. где Emin и Emax - наименьшее и наибольшее значения освещенности в И стандартного тест-объекта; за такой объект обычно принимают решетку, яркость которой меняется по синусоидальному закону с частотой R (число периодов решетки на мм). К зависит от R и направления штрихов решетки. Функция k(R) называется частотно-контрастной характеристикой. В идеальных системах k равен нулю при К = 2А" /lи более, где A" - числовая апертура системы в пространстве изображений, l - длина волны света. Чем меньше k при заданной R, тем хуже качество И в данной системе.
Лит.: Тудоровский А. И., Теория оптических приборов, 2 изд., (ч.) 1, М. - Л., 1948, гл. 8, 10, 14: Слюсарев Г. Г., Методы расчета оптических систем, 2 изд., Л., 1969.
Г. Г. Слюсарев.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 09.03.2026 22:22:43
|

|

|
 |
|

|
 |
 |
 |
|