
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Излучение | Излучение (далее И) электромагнитное, процесс образования свободного электромагнитного поля. (Термин "И" применяют также для обозначения самого свободного, т. е. излученного, электромагнитного поля - см. Максвелла уравнения, Электромагнитные волны.) Классическая физика рассматривает И как испускание электромагнитных волн ускоренно движущимися электрическими зарядами (в частности, переменными токами). Классическая теория объяснила очень многие характерные черты процессов И, однако она не смогла дать удовлетворительного описания ряда явлений, особенно теплового излучения тел и И микросистем ( и молекул). Такое описание оказалось возможным лишь в рамках квантовой теории И, показавшей, что И представляет собой рождение фотонов при изменении состояния квантовых систем (например, Квантовая теория, более глубоко проникнув в природу И, одновременно указала и границы применимости классической теории: последняя часто является очень хорошим приближением при описании И, оставаясь, например, теоретической базой радиотехники (см. И и прием радиоволн).
Классическая теория излучения (теория Максвелла). Физические причины существования свободного электромагнитного поля (т. е. поля самоподдерживающегося, независимого от возбудивших его источников) тесно связаны с тем, что электромагнитные волны распространяются от источников - зарядов и токов - не мгновенно, а с конечной скоростью c (в вакууме c @ 3·1010 см/сек). Если источник И (например, переменный ток) в какой-то момент исчезнет, это не приведет к мгновенному исчезновению поля во всем пространстве: в отдаленных от источника точках оно исчезнет лишь через конечный промежуток времени. Из теории Максвелла вытекает, что изменение во времени электрического поля Е порождает поле Н, а изменение Н - вихревое электрическое поле. Отсюда следует, что самоподдерживающимся может быть лишь переменное электромагнитное поле, в котором обе его компоненты - Е и Н, непрерывно изменяясь, постоянно возбуждают одна другую.
В процессе И электромагнитное поле уносит от источника энергию. Плотность потока энергии этого поля (количество энергии, протекающей за единицу времени через единичную площадку, ориентированную перпендикулярно направлению потока) определяется Пойнтинга вектором П, который пропорционален векторному произведению (ЕН).
Интенсивность И Eизл есть энергия, уносимая полем от источника в единицу времени. Порядок ее величины можно оценить, вычислив произведение площади замкнутой поверхности, охватывающей источник на среднее значение абсолютной величины плотности потока П на этой поверхности (П ~ EH). Обычно поверхность выбирают в форме сферы радиуса R (ее площадь ~ R) и вычисляют Eизл в пределе R R ¥:
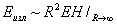 (1) (1)
(Е и Н - абсолютные величины векторов Е и Н).
Для того чтобы эта величина не обращалась в ноль, т. е. чтобы вдали от источника существовало свободное электромагнитное поле, необходимо, чтобы и Е, и Н убывали не быстрее, чем 1/R. Это требование удовлетворяется, если источниками полей являются ускоренно движущиеся заряды. Вблизи от зарядов поля - кулоновские, пропорциональные 1/R2, но на больших расстояниях основную роль начинают играть некулоновские поля Е и Н, имеющие закон убывания 1/R.
И движущегося заряда. Простейшим источником поля является точечный заряд. У покоящегося заряда И отсутствует. Равномерно движущийся заряд (в пустоте) также не может быть источником И Заряд же, движущийся ускоренно, излучает. Прямые вычисления на основе уравнений Максвелла показывают, что интенсивность его И равна
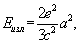 (2) (2)
где е - величина заряда, a - его ускорение. (Здесь и ниже используется Гауссова система единиц, см. СГС система единиц.) В зависимости от физической природы ускорения И иногда приобретает особые наименования. Так, И, возникающее при торможении заряженных частиц в веществе в результате воздействия на них кулоновских полей ядер и электронов называется тормозным излучением. И заряженной частицы, движущейся в поле, искривляющем ее траекторию, называется синхротронным излучением (или И). Оно наблюдается, например, в циклических ускорителях заряженных частиц.
В частном случае, когда заряд совершает гармоническое колебание, ускорение а по величине равно произведению отклонения заряда от положения равновесия (х = x0 sin wt, x0 - амплитуда отклонения х) на квадрат частоты w. Усредненная по времени t интенсивность И
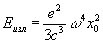 (3) (3)
очень быстро (пропорционально w4) растет при увеличении частоты.
Электрическое дипольное И Простейшей системой, которая может быть источником И, являются два связанных друг с другом колеблющихся, равных по величине, разноименных заряда. Они образуют диполь с переменным моментом. Если, например, заряды диполя совершают гармонические колебания навстречу друг другу, то дипольный электрический момент изменяется по закону d = d0 sin wt (w - частота колебаний, d0 - амплитуда момента d). Усредненная по времени t интенсивность И такого диполя
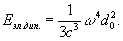 (4) (4)
И, расходящееся от колеблющегося диполя, неизотропно, т. е. энергия, испускаемая им в различных направлениях, неодинакова. Вдоль оси колебаний И вообще отсутствует. Под прямым же углом к оси колебаний И максимально. Для всех промежуточных направлений угловое распределение И меняется пропорционально sin2 J, где угол J отсчитывается от направления оси колебаний. Если направление оси колебаний диполя меняется со временем, то усредненное угловое распределение становится более сложным.
Реальные излучатели, как правило, включают множество зарядов. Точный учет всех деталей движения каждого из них при исследовании И излишен (а зачастую и невозможен). Действительно, И определяется значениями полей вдали от источника, т. е. там, где детали распределения зарядов (и токов) в излучателе сказываются слабо. Это позволяет заменять истинное распределение зарядов приближенным. Самым грубым, "нулевым" приближением является рассмотрение излучающей системы как одного заряда, по величине равного сумме зарядов системы. У электронейтральной системы, сумма зарядов которой равна нулю, И в этом приближении отсутствует. В следующем, первом, приближении положительные и отрицательные заряды системы по отдельности мысленно "стягиваются" к центрам своего распределения. Для электронейтральной системы это означает мысленную замену ее электрическим диполем, излучающим согласно (4). Такое приближение называется дипольным, а соответствующее И - электрическим дипольным И
Электрическое квадрупольное и высшие мультипольные И Если у системы зарядов дипольное И отсутствует, например из-за равенства дипольного момента нулю, то необходимо учитывать следующее приближение, в котором система зарядов - источник И - рассматривается как квадруполь, т. е. четырехполюсник. Простейший квадруполь - 2 диполя, имеющие равные по величине и противоположные по направлению моменты. Еще более детальное описание излучающей системы зарядов дает рассмотрение последующих приближений, в которых распределение зарядов описывается мультиполями (многополюсниками) высших порядков (диполь называется мультиполем 1-го, квадруполь - 2-го и т. д. порядков).
Важно отметить, что в каждом последующем приближении интенсивность И примерно в (v/c)2 меньше, чем в предыдущем (если, конечно, последнее не отсутствует по каким-либо причинам). Если излучатель - нерелятивистский, т. е. все заряды имеют скорости, много меньшие, чем световая (v/c << 1), то главную роль играет низшее неисчезающее приближение. Так, если имеется дипольное И, оно является основным, а все остальные высшие мультипольные поправки крайне малы и их можно не учитывать. В случае же И релятивистских частиц описание И с помощью мультиполей становится неэффективным, так как вклад мультиполей высших порядков перестает быть малым.
дипольное И Кроме электрических диполей и высших мультиполей, источниками И могут быть также диполи и мультиполи (как правило, основным является дипольное И). Картина распределения поля на больших расстояниях от контура, по которому протекает ток, порождающий это поле, подобна картине распределения электрического поля вдали от электрического диполя. Аналог дипольного электрического момента - дипольный момент М - определяется силой тока в контуре и его геометрией. Для плоского контура абсолютная величина момента М = (e/c) , где - площадь, охватываемая контуром. Формулы для интенсивности дипольного И почти такие же, как и для электрического, только вместо электрического дипольного момента d в них стоит момент М. Так, если момент изменяется по гармоническому закону М = M0 sin wt (для этого должна гармонически меняться сила тока в контуре), то усредненная по времени интенсивность И равна:
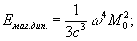 (5) (5)
здесь M0 - амплитуда момента M.
Отношение дипольного момента к электрическому имеет порядок v/c, где v - скорость движения зарядов, образующих ток; отсюда вытекает, что интенсивность дипольного И в (v/c)2 раз меньше, чем дипольного электрического, если, конечно, последнее присутствует. Таким образом, интенсивности дипольного и электрического квадрупольного И имеют одинаковый порядок величины.
И релятивистских частиц. Одним из важнейших примеров такого И является синхротронное И заряженных частиц в циклических (кольцевых) ускорителях. Резкое отличие от нерелятивистского И проявляется здесь уже в спектральном составе И: если частота обращения заряженной частицы в ускорителе равна w (нерелятивистский излучатель испускал бы волны такой же частоты), то интенсивность ее И имеет максимум при частоте wмакс ~ g3w, где g = (1 - (v/c)2)-1/2, т. е. основная доля И при v R с приходится на частоты, более высокие, чем w. Такое И направлено почти по касательной к орбите частицы, в основном вперед по направлению ее движения.
Ультрарелятивистская частица может излучать электромагнитные волны, даже если она движется прямолинейно и равномерно (но только в веществе, а не в пустоте!). Это И, названное Черенкова - Вавилова излучением, возникает, если скорость заряженной частицы в среде превосходит фазовую скорость света в этой среде (uфаз = c/n, где n - показатель преломления среды). И появляется из-за того, что частица "перегоняет" порождаемое ею поле, отрывается от него.
Квантовая теория излучения. Выше уже говорилось, что классическая теория дает лишь приближенное описание процессов И (весь физический мир в принципе является "квантовым"). Однако существуют и такие физические системы, И которых невозможно даже приближенно описать в согласии с опытом, оставаясь на позициях классической теории. Важная особенность таких квантовых систем, как или молекула, заключается в том, что их внутренняя энергия не меняется непрерывно, а может принимать лишь определенные значения, образующие дискретный набор. Переход системы из состояния с одной энергией в состояние с другой энергией (см. Квантовые переходы) происходит скачкообразно; в силу закона сохранения энергии система при таком переходе должна терять или приобретать определенную "порцию" энергии. Чаще всего этот процесс реализуется в виде испускания (или поглощения) системой кванта И - фотона. Энергия кванта eg = _w, где _ - Планка постоянная (_ = 1,05450×10-27 эрг×сек), w - круговая частота. Фотон всегда выступает как единое целое, испускается и поглощается "целиком", в одном акте, имеет определенную энергию, импульс и спин (проекцию момента количества движения на направление импульса), т. е. обладает рядом корпускулярных свойств. В то же время фотон резко отличается от обычных классических частиц тем, что у него есть и волновые черты. Такая двойственность фотона представляет собой частное проявление корпускулярно-волнового дуализма.
Последовательной квантовой теорией И является квантовая электродинамика (см. Квантовая теория поля). Однако многие результаты, относящиеся к процессам И квантовых систем, можно получить из более простой полуклассической теории И Формулы последней, согласно соответствия принципу, при определенном предельном переходе должны давать результаты классической теории. Таким образом, устанавливается глубокая аналогия между величинами, характеризующими процессы И в квантовой и классической теориях.
И Система из ядра и движущегося в его кулоновском поле электрона должна находиться в одном из дискретных состояний (на определенном уровне энергии). При этом все состояния, кроме основного (т. е. имеющего наименьшую энергию), неустойчивы. находящийся в неустойчивом (возбужденном) состоянии, даже если он изолирован, переходит в состояние с меньшей энергией. Этот квантовый переход сопровождается испусканием фотона; такое И называется спонтанным (самопроизвольным). Энергия, уносимая фотоном eg = _w, равна разности энергии начального i и конечного j состояний (ei > ej, eg = ei - ej); отсюда вытекает формула Н. Бора для частот И:
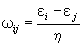 (6) (6)
Важно отметить, что такие характеристики спонтанного И, как направление распространения (для совокупности - угловое распределение их спонтанного И) и поляризация, не зависят от И других объектов (внешнего электромагнитного поля).
Формула Бора (6) определяет дискретный набор частот (и следовательно, длин волн) И Она объясняет, почему спектры И имеют хорошо известный "линейчатый" характер - каждая линия спектра соответствует одному из квантовых переходов данного вещества.
Интенсивность И В квантовой теории, как и в классической, можно рассматривать электрические дипольное и высшие мультипольные И Если излучатель нерелятивистский, основным является электрическое дипольное И, интенсивность которого определяется формулой, близкой к классической:
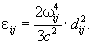 (7) (7)
Величины dij, являющиеся квантовым аналогом электрического дипольного момента, оказываются отличными от нуля лишь при определенных соотношениях между квантовыми числами начального i и конечного j состояний (правила отбора для дипольного И). Квантовые переходы, удовлетворяющие таким правилам отбора, называются разрешенными (фактически имеется в виду разрешенное электрическое дипольное И). Переходы же высших мультипольностей называются запрещенными. Этот запрет относителен: запрещенные переходы имеют относительно малую вероятность, т. е. отвечающая им интенсивность И невелика. Те состояния, переходы из которых "запрещены", являются сравнительно устойчивыми (долгоживущими). Они называются метастабильными состояниями.
Квантовая теория И позволяет объяснить не только различие в интенсивностях разных линий, но и распределение интенсивности в пределах каждой линии; в частности, ширину спектральных линий.
Источниками электромагнитного И могут быть не только но и более сложные квантовые системы. Общие методы описания И таких систем те же, что и при рассмотрении но конкретные особенности И весьма разнообразны. И молекул, например, имеет более сложные спектры, чем И Для И ядер типично, что энергия отдельных квантов обычно велика (g-кванты), интенсивность же И сравнительно низка (см. Гамма-излучение, Ядро атомное).
Электромагнитное И часто возникает и при взаимных превращениях элементарных частиц (аннигиляции электронов и позитронов, распаде нейтрального пи-мезона и т. д.).
Вынужденное И Если частота внешнего И, падающего на уже возбужденный совпадает с одной из частот возможных для этого согласно (6) квантовых переходов, то испускает квант И, в точности такой же, как и налетевший на него (резонансный) фотон. Это И называется вынужденным. По своим свойствам оно резко отличается от спонтанного - не только частота, но и направление распространения, и поляризация испущенного фотона оказываются теми же, что у резонансного. Вероятность вынужденного И (в отличие от спонтанного!) пропорциональна интенсивности внешнего И, т. е. количеству резонансных фотонов. Существование вынужденного И было постулировано А. Эйнштейном при теоретическом анализе процессов теплового И тел с позиций квантовой теории и затем было подтверждено экспериментально. В обычных условиях интенсивность вынужденного И мала по сравнению с интенсивностью спонтанного. Однако она сильно возрастает в веществе, в котором в метастабильном состоянии находится больше чем в одном из состояний с меньшей энергией (в которое возможен квантовый переход). При попадании в такое вещество резонансного фотона испускаются фотоны, в свою очередь играющие роль резонансных. Число излучаемых фотонов лавинообразно возрастает; результирующее И состоит из фотонов, совершенно идентичных по своим свойствам, и образует когерентный поток (см. Когерентность). На этом явлении основано действие квантовых генераторов и квантовых усилителей И
Роль теории излучения. Практическое и научно-прикладное значение теории И огромно. На ней основывается разработка и применение лазеров и мазеров, создание новых источников света, ряд важных достижений в области радиотехники и спектроскопии. Понимание и изучение законов И важно и в другом отношении: по характеру И (энергетическому спектру, угловому распределению, поляризации) можно судить о свойствах излучателя. И - пока фактически единственный и весьма многосторонний источник информации о космических объектах. Например, анализ И, приходящего из космоса, привел к открытию таких необычных небесных тел, как пульсары. Изучение спектров далеких внегалактических объектов подтвердило теорию расширяющейся Вселенной. Одновременно изучение И позволяет проникнуть в область явлений микромира. Именно теории И принадлежит особая роль в формировании всей современной физической картины мира: преодоление трудностей, возникших в электродинамике движущихся сред, привело к созданию относительности теории; исследования М. Планка, посвященные тепловому излучению, положили начало квантовой теории и квантовой механике. Дальнейшее развитие теории И должно привести к еще более глубокому познанию материи.
Лит.: Тамм И Е., Основы теории электричества, 7 изд., М., 1957; Иваненко Д., Соколов А., Классическая теория поля, М. - Л., 1949; их же, Квантовая теория поля, М. - Л., 1952; Ахиезер А. И, Берестецкий В. Б., Квантовая электродинамика, 2 изд., М., 1959; Ландау Л. Д., Лифшиц Е. М., Теория поля, 5 изд., М., 1967 (Теоретическая физика, т. 2).
В. И Григорьев. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 09.03.2026 22:18:39
|

|

|
 |
|

|
 |
 |
 |
|