
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Извлечение корня | Извлечение корня (далее И) алгебраическое действие, обратное возведению в степень. Извлечь корень n-й степени из числа а - это значит найти такое число (или числа) x, которое при возведении в n-ю степень даст данное число (xn = а); число х (обозначается 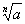 ) называется корнем, n - показателем корня, а - подкоренным выражением. Знак ) называется корнем, n - показателем корня, а - подкоренным выражением. Знак 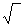 есть измененное написание буквы r (лат. radix - корень). Например, есть измененное написание буквы r (лат. radix - корень). Например, 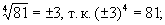 среди мнимых чисел имеются еще два корня среди мнимых чисел имеются еще два корня 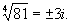 Корень 2-й степени называется квадратным (обозначается Корень 2-й степени называется квадратным (обозначается 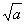 ), корень 3-й степени - кубическим. Задача И n-й степени из числа а эквивалентна решению двучленного уравнения xn - а = 0. Это уравнение имеет n решений, следовательно, существует n корней из числа а. Если а - действительное положительное число, то один из корней (называемый арифметическим) будет также действительным и положительным; под задачей И часто понимают нахождение именно арифметического корня. Корни из рациональных чисел не всегда рациональны, поэтому возникает вопрос о нахождении их приближенных значений. При вычислении корней пользуются логарифмическими таблицами или специальными таблицами корней. См. также Корень. ), корень 3-й степени - кубическим. Задача И n-й степени из числа а эквивалентна решению двучленного уравнения xn - а = 0. Это уравнение имеет n решений, следовательно, существует n корней из числа а. Если а - действительное положительное число, то один из корней (называемый арифметическим) будет также действительным и положительным; под задачей И часто понимают нахождение именно арифметического корня. Корни из рациональных чисел не всегда рациональны, поэтому возникает вопрос о нахождении их приближенных значений. При вычислении корней пользуются логарифмическими таблицами или специальными таблицами корней. См. также Корень.
Лит.: Брадис В. М., Четырехзначные математические таблицы, 41 изд., М., 19703 Барлоу П., Таблицы квадратов, кубов, квадратных корней, кубических корней и обратных величин всех целых чисел до 12500, М., 1965. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 09.03.2026 22:20:17
|

|

|
 |
|

|
 |
 |
 |
|