
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Звездная статистика | Звездная статистика (далее З) раздел звездной астрономии, изучающий методами математической статистики пространственное распределение звезд, обладающих сходными физическими характеристиками, и различные статистические зависимости между характеристиками звезд. Начало З было положено В. Гершелем, который в конце 18 в. обнаружил рост числа звезд, видимых в его телескоп, по мере приближения к плоскости Млечного Пути (т. н. галактическая концентрация) и объяснил это сплюснутостью нашей Галактики. Одной из важных задач З является определение звездной плотности D (r), т. е. числа звезд в единице объема в данном направлении на расстоянии r. При решении этой задачи чаще всего используются статистические методы, т. к. непосредственно определить расстояние можно либо до ближайших к Солнцу объектов (r < 100nc), либо до некоторых особых типов звезд, например переменных звезд.
Широкое применение в З получили дифференциальная функция распределения звезд по видимым звездным величинам А (м) и интегральная функция (m), указывающая число звезд ярче данной звездной величины m, а также функция распределения звезд по их абсолютным звездным величинам, т. н. функция светимости j(М). Функции А (м) и (m) непосредственно определяются по подсчетам звезд данной видимой величины или звезд ярче этой величины. Функцию светимости можно определить путем решения интегральных уравнений З Функция А (м) связана с функцией звездной плотности D (r) и функцией светимости j(М) соотношением (первое интегральное уравнение З):
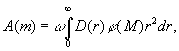
где w - выбранный телесный угол. С помощью среднего параллакса
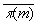
звезд видимой величины m выводится соотношение (второе интегральное уравнение З):
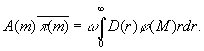
Эти уравнения используются как для определения D (r), так и j(М). Чаще всего уравнения З решаются численными методами. Оба приведенных уравнения называются уравнениями Шварцшильда (по имени немецкого астронома К. Шварцшильда, который вывел их в 1910).
В предположении существования межзвездного поглощения света интегральные уравнения сохраняют свой вид, но в результате их решения получается видимая звездная плотность D"(r), с помощью которой, если известна зависимость поглощения света от расстояния, т. е. функция поглощения света А (r), можно определить истинную звездную плотность D (r).
При исследовании распределения небесных объектов удобен метод, предложенный в 1937 советским астрономом М. А. Вашакидзе и независимо от него голландским астрономом Я. Оортом в 1938. Этот метод позволяет исследовать распределение звездной плотности в произвольном направлении, если известно ее распределение в направлении, перпендикулярном галактической плоскости. Таким путем установлено, что звездная плотность имеет общую тенденцию расти в направлении на центр Галактики, а Солнце располагается между двумя местными сгущениями, которые можно отождествить со спиральными ветвями Галактики.
Метод Вашакидзе - Оорта был применен советским астрономом Б. В. Кукаркиным (1947) для исследования пространственного распределения переменных звезд. Было показано, что различные типы переменных звезд характеризуются различной степенью концентрации к плоскости Галактики и к галактическому центру, причем параметры пространственного распределения звезд связаны с их кинематическими характеристиками (см. Звездные подсистемы).
Лит. см. при ст. Звездная астрономия.
Е. Д. Павловская.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 11.03.2026 17:41:08
|

|

|
 |
|

|
 |
 |
 |
|