
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Звездная кинематика | Звездная кинематика (далее З) раздел звездной астрономии, изучающий статистическими методами закономерности движения различных объектов в Галактике. З изучает движения звезд, освобожденные от эффектов, связанных с вращением Земли, ее обращением вокруг Солнца, нутацией, прецессией и т.п. Основными кинематическими характеристиками галактических объектов являются их собственные движения m"a, m"d (см. Собственное движение звезды) и лучевые скорости vr, которые связаны с пространственной скоростью звезды v относительно Солнца соотношением:
v2 =(4,74m"ar)2 + (4,74m"dr)2 + vr2,
где r - расстояние от звезды до Солнца (здесь r и v выражены в км/сек, r - в nc). Движение любой группы звезд в пространстве можно характеризовать ее средним движением (движением центроида группы) относительно Солнца и параметрами распределения остаточных скоростей, т. е. разностей скоростей звезд центроида.
До начала 20 в. предполагалось, что распределение остаточных скоростей звезд хаотично. Однако уже первые статистические исследования обнаружили неравномерность различных направлений движения звезд в Галактике. Математическую теорию распределения пекулярных скоростей разработал нем. астроном К. Шварцшильд, предположивший, что функция распределения пекулярных скоростей имеет вид:
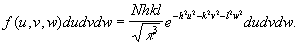
Величины h, k, l характеризуют дисперсии компонентов скоростей в направлении гл. осей u, v, w, - число исследуемых звезд. Поверхностями равной плотности концов векторов скоростей являются в общем случае трехосные эллипсоиды, направления больших полуосей которых близки к направлению на центр Галактики.
Отношения полуосей, пропорциональных дисперсиям остаточных скоростей, примерно постоянны для различных групп звезд и составляют 1: 0,6: 0,5. Однако их абсолютные значения зависят от того, к какой составляющей Галактики принадлежат исследуемые объекты. Так, для звезд спектральных классов О и В - типичных представителей плоской составляющей средняя квадратичная скорость равна приблизительно 10км/сек, а для объектов сферической составляющей - порядка 100 км/сек. Эти различия являются следствием неодинаковых условий формирования и возраста звезд разных составляющих.
Скорость Солнца v0 может быть определена путем анализа движений различных групп звезд. По отношению к видимым невооруженным глазом звездам Солнце движется со скоростью v0 = 19,5 км/сек в направлении: прямое восхождение 18 ч, склонение около + 30° (т. н. стандартный апекс). Относительно некоторых др. групп звезд v0 достигает "140 км/сек. Разность скоростей Солнца относительно двух центроидов характеризует взаимное движение центроидов, подчиненное определенным закономерностям. Проекции концов векторов скорости Солнца для различных групп звезд на галактическую плоскость располагаются примерно на одной прямой, проходящей в направлении галактических долгот 90°-270°. Объяснение этой закономерности дал шведский астроном Б. Линдблад, предположив, что Галактика состоит из взаимопроникающих подсистем, вращающихся с разными скоростями вокруг одной и той же оси, проходящей через центр Галактики перпендикулярно к ее плоскости. Звезды, относительно которых Солнце имеет скорость 19,5 км/сек, вращаются наиболее быстро. Исследование вращения Галактики показывает, что на расстоянии Солнца оно происходит по законам, промежуточным между законами вращения твердого тела и законами Кеплера (ближе к последним). Влияние дифференциального эффекта вращения Галактики на компоненты собственных движений D(l и Dmb в галактических координатах l и b и лучевые скорости Dvr для звезд в пределах около 1 knc от Солнца выражаются формулами, предложенными голландским астрономом Я. Оортом (1927):
Dvr = sin 21 cos2b; D(l = A cos 2l + В;
Dmb = - sin 21 sin b cos b.
Вращение Галактики на расстоянии Солнца может быть описано следующими значениями параметров (постоянных Оорта): А = 15 (км/сек)/кnc; В = - 10 (км/сек)/кnc.
Лит. см. при ст. Звездная астрономия.
Е. Д. Павловская.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 11.03.2026 19:23:39
|

|

|
 |
|

|
 |
 |
 |
|