
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Дробно-линейная функция | Дробно-линейная функция (далее Д) функция вида
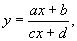
т. е. частное двух линейных функций. Д.-л. ф. - простейшая среди рациональных функций. При ad - bc = 0 она сводится к тождественной постоянной; если ad - bc ¹ 0, но с = 0, то Д.-л. ф. сводится к целой линейной функции у = aх + b. Т. о., интерес представляет лишь случай, когда ad - bc ¹ 0 и с ¹ 0; графиком Д.-л. ф., когда х принимает действительные значения, является равнобочная гипербола.
Если х принимает произвольные комплексные значения (а, b, с и d - фиксированные комплексные числа), то Д.-л. ф. осуществляет взаимно однозначное и конформное отображение комплексной плоскости (пополненной точкой ¥) на себя, называемое дробно-линейным отображением (это единственная аналитическая функция, обладающая указанным свойством). Д.-л. ф. характеризуется также тем, что она переводит прямые и окружности, лежащие в комплексной плоскости, снова в прямые и окружности. Всякое конформное отображение внутренности круга на себя осуществляется при помощи Д.-л. ф. Двойное отношение четырех точек
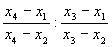
является инвариантом Д.-л. ф. Иными словами, если Д.-л. ф. переводит x1 в y1, x2 в y2, x3 в у3 и x4 в y4, то
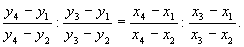
Лит.: Маркушевич А. И., Краткий курс теории аналитических функций, 3 изд., М., 1966; Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967.
С. Б. Стечкин.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 16:27:51
|

|

|
 |
|

|
 |
 |
 |
|