
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Длина | Длина (далее Д) числовая характеристика протяженности линий. В разных случаях понятие Д определяется различно. 1) Д отрезка прямой - расстояние между его концами, измеренное каким-либо отрезком, принятым за единицу Д 2) Д ломаной - сумма Д ее звеньев. 3) Д простой дуги - предел Д вписанных в эту дугу ломаных, когда число звеньев неограниченно увеличивается и максимальная Д звеньев стремится к нулю. 4) Д непрерывной кривой, состоящей из конечного числа простых дуг, равна сумме Д этих дуг. Например, Д окружности может быть получена как предел периметров правильных вписанных многоугольников при неограниченном удвоении числа их сторон и равна 2pR, где R - радиус окружности. Всякая непрерывная кривая имеет Д - конечную или бесконечную. Если ее Д конечна, то кривая называется спрямляемой. График функции (см. рис.)
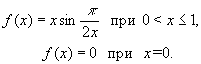
дает пример неспрямляемой кривой; здесь Д вписанных ломаных неограниченно растут, когда Д звеньев стремятся к нулю. Если уравнение плоской кривой в прямоугольных координатах имеет вид у = f (x) (a £ x £ b), причем функция f (x) имеет непрерывную производную f¢ (x), то Д кривой выражается интегралом
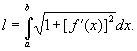
Аналогично выражается Д кривой, заданной параметрически, и Д пространственной кривой.
К вычислению Д кривой при помощи предельного перехода из Д ломаных прибегали по существу еще математики древности. Для них, однако, этот предельный переход был лишь способом вычисления Д кривой, а не определения понятия Д кривой, т.к. последнее им представлялось, по-видимому, одним из первоначальных математических понятий. Необходимость определения Д кривой стала ясной лишь в 1-й половине 19 в. Полное выяснение вопроса было достигнуто К. Жорданом. В дифференциальной геометрии определяется также Д кривой на поверхности или в произвольном римановом пространстве. О единицах и технике измерения Д см. Меры длины, Измерение.
Лит.: Лебег А., Об измерении величин, пер. с франц., 2 изд., М., 1960; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969.
С. Б. Стечкин.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 14:39:21
|

|

|
 |
|

|
 |
 |
 |
|