
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Дифференциальный бином | Дифференциальный бином (далее Д)биномиальный дифференциал, выражение вида
xm (а + bxn)pdx,
где а и b - постоянные, отличные от нуля, m, n и р - рациональные числа. Интеграл от Дифференциальный бином
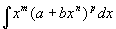
выражается в конечном виде через элементарные функции лишь в трех случаях: 1) если р - целое число; 2) если (m + 1)/n - целое число; 3) если ((m + 1)/n)+p - целое число. Эти три случая интегрируемости Дифференциальный бином были известны еще Л. Эйлеру. П. Л. Чебышев в 1853 показал, что во всех остальных случаях интеграл от Дифференциальный бином в конечном виде через элементарные функции не выражается. Это один из первых случаев, когда вопрос об интегрируемости в конечном виде какого-либо достаточно общего класса аналитических выражений был решен до конца. Результат Чебышева может быть поставлен в ряд с классическими теоремами о невозможности алгебраического решения различных классов алгебраических уравнений и о неразрешимости при помощи циркуля и линейки задачи о квадратуре круга.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 14:35:34
|

|

|
 |
|

|
 |
 |
 |
|