
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Дифференциальные уравнения | Дифференциальные уравнения (далее Д) уравнения, содержащие искомые функции, их производные различных порядков и независимые переменные. Теория Д возникла в конце 17 в. под влиянием потребностей механики и других естественнонаучных дисциплин, по существу одновременно с интегральным исчислением и дифференциальным исчислением.
Простейшие Д встречались уже в работах И. Ньютона и Г. Лейбница; термин "Д" принадлежит Лейбницу. Ньютон при создании исчисления флюксий и флюент (см. Флюксий исчисление) ставил две задачи: по данному соотношению между флюентами определить соотношение между флюксиями; по данному уравнению, содержащему флюксии, найти соотношение между флюентами. С современной точки зрения, первая из этих задач (вычисление по функциям их производных) относится к дифференциальному исчислению, а вторая составляет содержание теории обыкновенных Д Задачу нахождения неопределенного интеграла (x) функции f (x) Ньютон рассматривал просто как частный случай его второй задачи. Такой подход был для Ньютона как создателя основ математического естествознания вполне оправданным: в очень большом числе случаев законы природы, управляющие теми или иными процессами, выражаются в форме Д, а расчет течения этих процессов сводится к решению Д
Следующие два простых примера могут служить иллюстрацией к сказанному.
1) Если тело, нагретое до температуры Т, помещено в среду, температура которой равна нулю, то при известных условиях можно считать, что приращение DТ (отрицательное в случае T > 0) его температуры за малый промежуток времени Dt с достаточной точностью выражается формулой
DT = -kTDt,
где k - постоянный коэффициент. При математической обработке этой физической задачи считают, что выполняется точно соответствующее предельное соотношение между дифференциалами
dT = -kTdt, (1)
т. е. имеет место Д
T" = -kT,
где T" (обозначает производную по t. Решить полученное Д, или, как выражаются иначе, проинтегрировать его, значит найти функции, обращающие его в тождество. Для уравнения (1) все такие функции (т. е. все его частные решения) имеют вид
Т = -kt, (2)
где С постоянно. Сама формула (2) с произвольной постоянной С называется общим решением уравнения (1).
2) Пусть, например, груз р массы m подвешен к пружине и находится в положении равновесия (рис. 1, а). Отклоняя его от положения равновесия с помощью растяжения пружины (рис. 1, б), приводят груз в движение. Если x (t) обозначает величину отклонения тела от положения равновесия в момент времени t, то ускорение тела выражается 2-й производной x" (t). Сила mх" (t), действующая на тело, при небольших растяжениях пружины по законам теории упругости пропорциональна отклонению x (t). Т. о., получается Д
mх" (t) = - kx (t). (3)
Его решение имеет вид:
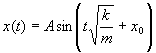
и показывает, что тело будет совершать гармонические колебания (рис. 1, в).
Теория Д выделилась в самостоятельную детально разработанную научную дисциплину в 18 в. (труды Д. Бернулли, Ж. Д" Аламбера и особенно Л. Эйлера).
Д делятся на "обыкновенные", содержащие производные одной или нескольких функций одного независимого переменного, и "уравнения с частными производными", содержащие частные производные функций нескольких независимых переменных. Порядком Д называется наибольший порядок входящих в него производных. Так, например,
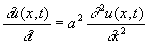
есть Д с частными производными 2-го порядка.
Обыкновенные дифференциальные уравнения. Уравнения 1-го порядка. Обыкновенным Д 1-го порядка с одной неизвестной функцией (только такие пока будут рассматриваться) называется соотношение
(x, у, у") = 0 (А)
между независимым переменным х, искомой функцией у и ее производной
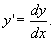
Если уравнение (А) может быть разрешено относительно производной, то получается уравнение вида
y" = f (x, у). (Б)
Многие вопросы теории Д проще рассматривать для таких разрешенных относительно производной уравнений, предполагая функцию f (x, y) однозначной.
Уравнение (Б) можно записать в виде соотношения между дифференциалами
f (x, y) dx - dy = 0,
тогда оно становится частным случаем уравнений вида
Р (х, у) dx + Q (x, у) dy = 0. (В)
В уравнениях вида (В) естественно считать переменные х и у равноправными, т. е. не интересоваться тем, какое из них является независимым.
Геометрическая интерпретация дифференциальных уравнений. Пусть у = у (х) есть решение уравнения (Б). Геометрически это значит, что в прямоугольных координатах касательная к кривой у = у (х) имеет в каждой лежащей на ней точке М (х, у) угловой коэффициент k = f (x, у). Т. о., нахождение решений у = у (х) геометрически сводится к такой задаче: в каждой точке некоторой области на плоскости задано "направление", требуется найти все кривые, которые в любой своей точке М имеют направление, заранее сопоставленное этой точке. Если функция f (x, у) непрерывна, то это направление меняется при перемещении точки М непрерывно, и можно наглядно изобразить поле направлений, проведя в достаточно большом числе достаточно густо расположенных по всей рассматриваемой области точек короткие черточки с заданным для этих точек направлением. На рис. 2 это выполнено для уравнения у" = у2. Рисунок позволяет сразу представить себе, как должны выглядеть графики решения - так называемые интегральные кривые Д Вычисление показывает, что общее решение данного уравнения есть
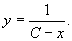
На рис. 2 вычерчены интегральные кривые, соответствующие значениям параметра С = 0 и С = 1.
График любой однозначной функции у = у (х) пересекает каждую прямую, параллельную оси Оу, только один раз. Таковы, следовательно, интегральные кривые любого уравнения (Б) с однозначной непрерывной функцией в правой части. Новые возможности для вида интегральных кривых открываются при переходе к уравнениям (В). При помощи пары непрерывных функций Р (х, у) и Q (x, у) можно задать любое непрерывное "поле направлений". Задача интегрирования уравнений (В) совпадает с чисто геометрической (не зависящей от выбора осей координат) задачей разыскания интегральных кривых по заданному на плоскости полю направлений. Следует заметить, что тем точкам (x0, у0), в которых обе функции Р (х, у) и Q (x, у) обращаются в нуль, не соответствует какое-либо определенное направление. Такие точки называются особыми точками уравнения (В).
Пусть, например, задано уравнение
ydx + xdy = 0,
которое можно записать в виде
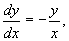
хотя, строго говоря, правая часть этого последнего уравнения теряет смысл при х = 0 и у = 0. Соответствующие поле направлений и семейство интегральных кривых, являющихся в этом случае окружностями х2 + у2 = С, изображены на рис. 3. Начало координат (х = 0, у = 0) - особая точка данного уравнения. Интегральными кривыми уравнения
ydx - xdy = 0,
изображенными на рис. 4, являются всевозможные прямолинейные лучи, выходящие из начала координат; начало координат является особой точкой и этого уравнения.
Начальные условия. Геометрическая интерпретация Д 1-го порядка приводит к мысли, что через каждую внутреннюю точку М области G с заданным непрерывным полем направлений можно провести одну вполне определенную интегральную кривую.
В отношении существования интегральной кривой сформулированная гипотеза оказывается правильной. Доказательство этого предложения принадлежит Дж. Пеано. В отношении же единственности интегральной кривой, проходящей через заданную точку, высказанная выше гипотеза оказывается, вообще говоря, ошибочной. Уже для такого простого уравнения, как
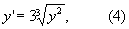
у которого правая часть непрерывна во всей плоскости, интегральные кривые имеют вид, изображенный на рис. 5. Единственность интегральной кривой, проходящей через заданную точку, нарушается здесь во всех точках оси Ox.
Единственность, т. е. однозначное определение интегральной кривой условием ее прохождения через заданную точку, имеет место для уравнений (Б) с непрерывной правой частью при том дополнительном условии, что функция f (х, у) имеет в рассматриваемой области ограниченную производную по у.
Это требование является частным случаем следующего, несколько более широкого условия Липшица: существует такая постоянная L, что в рассматриваемой области всегда
|f (x, y1) - f (x, y2)| < L |у1 - у2|.
Это условие чаще всего приводится в учебниках как достаточное условие единственности.
С аналитической стороны теоремы существования и единственности для уравнения вида (Б) обозначают следующее: если выполнены надлежащие условия (например, функция f (x, y) непрерывна и имеет ограниченную производную по у), то задание для "начального" значения x0 независимого переменного х "начального" значения у0 = у (x0) функции у (х) выделяет из семейства всех решений у (х) одно определенное решение. Например, если для рассмотренного выше уравнения (1) потребовать, чтобы в начальный момент времени t0 = 0 температура тела была равна "начальному" значению Т0, то из бесконечного семейства решений (2) выделится одно определенное решение, удовлетворяющее заданным начальным условиям:
T (t) = T0e-kt.
Этот пример типичен: в механике и физике Д обычно определяют общие законы течения какого-либо явления; однако, чтобы получить из этих законов определенные количественные результаты, надо присоединить к ним сведения о начальном состоянии изучаемой физической системы в некоторый определенный выбранный в качестве "начального" момент времени t0.
Если условия единственности выполнены, то решение y (x), удовлетворяющее условию у (x0) = у0, можно записать в виде:
y (x) = j(x; х0, у0), (5)
где x0 и у0 входят как параметры, функция же j (х; x0, y0) трех переменных х, x0 и y0 однозначно определяется самим уравнением (Б). Важно отметить, что при достаточно малом изменении поля (правой части Д) функция j(х; x0, у0) меняется сколь угодно мало на конечном промежутке изменения переменного х - имеется непрерывная зависимость решения от правой части Д Если правая часть f (x, у) Д непрерывна и ее производная по у ограничена (или удовлетворяет условию Липшица), то имеет место также непрерывность j(х; х0, у0) по x0 и y0.
Если в окрестности точки (х0, у0) для уравнения (Б) выполнены условия единственности, то все интегральные кривые, проходящие через достаточно малую окрестность точки (x0, у0), пересекают вертикальную прямую х = х0 и определяются ординатой у = С своей точки пересечения с этой прямой (см. рис. 6). Т. о., все эти решения содержатся в семействе с одним параметром С:
y (x) = (x, ),
которое является общим решением Д (Б).
В окрестности точек, в которых нарушаются условия единственности, картина может быть сложнее. Весьма сложен и вопрос о поведении интегральных кривых "в целом", а не в окрестности точки (x0, у0).
Общий интеграл. Особые решения. Естественно поставить обратную задачу: задано семейство кривых, зависящих от параметра С, требуется найти Д, для которого кривые заданного семейства служили бы интегральными кривыми. Общий метод для решения этой задачи заключается в следующем: считая семейство кривых на плоскости хОу заданным при помощи соотношения
(x, y, ) = 0, (6)
дифференцируют (6) при постоянном С и получают
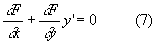
или в симметричной записи
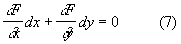
и из двух уравнений (6) и (7) или (6) и (8) исключают параметр С. Если данное Д получается таким образом из соотношения (6), то это соотношение называется общим интегралом заданного Д Одно и то же Д может иметь много различных общих интегралов. После нахождения для заданного Д общего интеграла оказывается необходимым, вообще говоря, еще исследовать, не имеет ли Д дополнительных решений, не содержащихся в семействе интегральных кривых (6).
Пусть, например, задано семейство кривых
(х -С)3 - у = 0. (9)
Дифференцируя (9) при постоянном С получают
3(х - С)2 - у" = 0,
после же исключения С приходят к Д
27y2 - (y ")3 = 0, (10)
равносильному уравнению (4). Легко видеть, что кроме решений (9), уравнение (10) имеет решение
y º 0. (11)
Решение уравнения (10) самого общего вида таково:
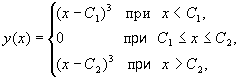
где -¥ £ 1 £ 2 £ +¥ (рис. 7). Оно зависит от двух параметров 1 и 2, но составляется из кусков кривых однопараметрического семейства (9) и куска особого решения (11).
Решение (11) уравнения (10) может служить примером особого решения Д В качестве другого примера можно рассмотреть семейство прямых
4(у - Cx) + 2= 0. (12)
Эти прямые являются интегральными кривыми Д
4(у - ху") + (у")2 = 0.
Особой же интегральной кривой этого Д служит парабола
х2 - у = 0,
огибающая прямые (12) (рис. 8). Картина, наблюдавшаяся в рассмотренном примере, типична; особые интегральные кривые обычно являются огибающими семейства интегральных кривых, получаемых из общего решения.
Д высших порядков и системы дифференциальных уравнений. Д n-го порядка с одной неизвестной функцией у (х) независимого переменного х записывают так:
(х, у, y", у", ..., y(n-1), y(n)) = 0. (13)
Если ввести дополнительные неизвестные функции
y1 = y", y2 = y", ..., yn-1 = y (n-1), (14)
то уравнение (13) можно заменить системой из n уравнений с n неизвестными функциями, но зато 1-го порядка. Для этого достаточно к n - 1 уравнениям (14) присоединить уравнение
(x, у, y1, у2, ..., yn-1, y"n-1) = 0.
Аналогичным образом сводятся к системам уравнений 1-го порядка и системы уравнений высших порядков. В механике сведение систем уравнений 2-го порядка к системе из удвоенного числа уравнений 1-го порядка имеет простой механический смысл. Например, система трех уравнений движения материальной точки
mx" = p (x, y, z), my" = Q (x, у, z),
mz" = R (x, у, z),
где х, у, z - координаты точки, зависящие от времени t, сводится к системе шести уравнений:
mu" = р (х, у, z), mv" = Q (x, у, z),
nw" = R (x, у, z), u = х", v = y", w = z"
при помощи введения в качестве новых переменных составляющих u, v, w скорости.
Наибольшее значение имеют системы, в которых число уравнений равно числу неизвестных функций. Система из n уравнений 1-го порядка с n неизвестными функциями, разрешенная относительно производных, имеет вид:
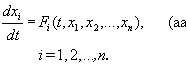
Решением системы Д (а) называется система функций x1(t), x2(t), ..., xn (t), которая при подстановке в уравнения (а) обращает их в тождества. Часто встречаются системы вида (а), в которых правые части не зависят от t. В этом случае изучение системы (а) в основном сводится к изучению системы из (n - 1)-го уравнения, которую целесообразно записывать в симметричной форме
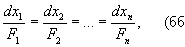
не предрешая вопроса о том, от какого из переменных х1, x2,..., xn мыслятся зависящими остающиеся n - 1 переменных. Считая х = (x1, x2,..., xn) вектором, можно записать систему (а) в виде одного векторного уравнения:
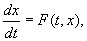
что позволяет широко пользоваться при изучении систем (а) аналогией с теорией одного уравнения 1-го порядка вида (Б). В частности, оказывается, что для систем (а) сохраняют силу основные результаты относительно существования и единственности решения задачи с начальными условиями: если в окрестности точки (t0, х10, x20, ..., xn0) все функции i непрерывны по совокупности переменных t, x1, x2, ..., xn и имеют ограниченные производные по переменным x1, x2, ..., xn, то задание начальных значений xi (t0) = xi0, i = 1, 2, ..., n, определяет одно, вполне определенное, решение системы (а). Этим объясняется то, что, вообще говоря, решение систем из n уравнений 1-го порядка с n неизвестными функциями зависит от n параметров.
Для приведенных выше конкретных примеров Д их общее решение удается выразить при помощи элементарных функций. Типы Д, допускающие такого рода решение, детально изучаются. Часто придерживаются более общей точки зрения, считая Д "решенным", если искомая зависимость между переменными (и входящими в общее решение параметрами c1, c2, ...) может быть выражена при помощи элементарных функций и одной или нескольких операций взятия неопределенного интеграла ("решение выражено в квадратурах").
Большой общностью обладают способы нахождения решений при помощи разложения их в степенные ряды. Например, если правые части уравнений (а) в окрестности точки (t0, x10, x20, ..., xn0) голоморфны (см. Аналитические функции), то решение соответствующей начальной задачи выражается функциями xi (t), разлагающимися в степенные ряды:
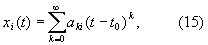
коэффициенты которых можно найти последовательным дифференцированием правых частей Д (а) и сопоставлением коэффициентов при одинаковых степенях в левых и правых частях этих уравнений.
Из специальных типов Д особенно хорошо разработана теория линейных Д и систем линейных Д (см. Линейные дифференциальные уравнения).
Для линейных Д сравнительно просто решаются также вопросы "качественного" поведения интегральных кривых, т. е. их поведение во всей области задания Д Для нелинейных Д, где нахождение общего решения особенно сложно, вопросы качественной теории Д приобретают иногда даже доминирующее значение. После классических работ А. М. Ляпунова ведущую роль в качественной теории Д играют работы советских математиков, механиков и физиков. В связи с этой теорией см. Динамическая система, Особая точка, Устойчивость, Предельный цикл.
Большое значение имеет аналитическая теория Д, изучающая решения Д с точки зрения теории аналитических функций, т. е. интересующаяся, например, расположением их особых точек в комплексной плоскости и т.п.
Наряду с рассмотренной выше начальной задачей, в которой задаются значения искомых функций (а в случае уравнений старших порядков и их производных) в одной точке (при одном значении независимого переменного), находят широкое применение краевые задачи.
Д с частными производными. Типичной особенностью Д с частными производными и систем Д с частными производными является то, что для однозначного определения частного решения здесь требуется задание не значений того или иного конечного числа параметров, а некоторых функций. Например, общим решением уравнения
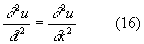
является выражение
u (t, x) = f (x + t) + g (x - t),
где f и g - произвольные функции. Т. о., Д (16) лишь в той мере ограничивает произвол в выборе функции двух переменных u (х, у), что ее удается выразить через две функции f (z) и g (v) от одного переменного, которые остаются (если в дополнение к уравнению (16) не дано каких-либо "начальных" или "краевых" условий) произвольными.
Типичной задачей с начальными условиями для системы Д с частными производными 1-го порядка
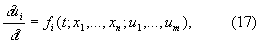
где независимыми переменными являются t, x1,..., xn, а u1,..., um суть функция от этих независимых переменных, может служить задача Коши: по заданным при каком-либо t = t0 значениям
ui (t0, x1,..., xn) = ji (x1,..., xn),
i = 1, 2, ..., m,
найти функции ui (t, x1, ..., xn).
В теории Д с частными производными порядка выше первого и систем Д с частными производными рассматриваются как задачи типа Коши, так и ряд краевых задач.
При постановке и решении краевых задач для Д с частными производными порядка выше первого существенное значение имеет тип уравнения. В качестве примера можно привести классификацию Д с частными производными 2-го порядка с одной неизвестной функцией z (х, у) от двух переменных:
(x, у, z, р, q, r, s, t) = 0, (18)
где
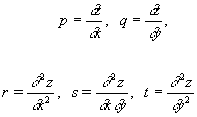
Если
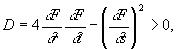
то (18) есть эллиптическое уравнение. Примером может служить уравнение Лапласа:
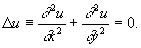
Если D < 0, то (18) есть гиперболическое уравнение. Примером может служить уравнение колебания струны:
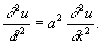
Если D = 0, то (18) есть параболическое уравнение. Примером может служить уравнение распространения тепла:
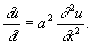
О краевых задачах для этих различных типов уравнений см. Уравнения математической физики.
Лит.: Обыкновенные Д Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959; Петровский И. Г., Лекции по теории обыкновенных дифференциальных уравнений, 5 изд., М., 1964; Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 2 изд., М., 1965; Камке Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем., 3 изд., М., 1965; Филиппов А. Ф., Сборник задач по дифференциальным уравнениям, 2 изд., М., 1965.
Д с частными производными. Петровский И. Г., Лекции об уравнениях с частными производными, 3 изд., М., 1961; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966; Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; Смирнов М. М., Задачи по уравнениям математической физики, 5 изд., М., 1968.
По материалам одноименной статьи из 2-го издания БСЭ.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 12:46:44
|

|

|
 |
|

|
 |
 |
 |
|