
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Дисперсия | Дисперсия (далее Д) (от лат. dispersio - рассеяние), в математической статистике и теории вероятностей, наиболее употребительная мера рассеивания, т. е. отклонения от среднего. В статистическом понимании Д
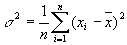
есть среднее арифметическое из квадратов отклонений величин xi от их среднего арифметического
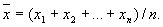
В теории вероятностей Д случайной величины Х называется математическое ожидание Е (Х - mх)2 квадрата отклонения Х от ее математического ожидания mх = Е (Х). Д случайной величины Х обозначается через D (X) или через s2X. Квадратный корень из Д (т. е. s, если Д есть s2) называется средним квадратичным отклонением (см. Квадратичное отклонение).
Для случайной величины Х с непрерывным распределением вероятностей, характеризуемым плотностью вероятности р (х), Д вычисляется по формуле
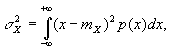
где
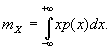
Об оценке Д по результатам наблюдения см. Статистические оценки.
В теории вероятностей большое значение имеет теорема: Д суммы независимых слагаемых равна сумме их Д Не менее существенно Чебышева неравенство, позволяющее оценивать вероятность больших отклонений случайной величины Х от ее математического ожидания.
Лит.: Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 14:56:21
|

|

|
 |
|

|
 |
 |
 |
|