
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Дирихле интеграл | Дирихле интеграл (далее Д) (по имени П. Г. Л. Дирихле), название интегралов нескольких типов.
1) Интеграл
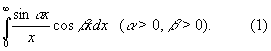
Этот Д называется также разрывным множителем Дирихле и равен p/2 при b < a, p/4 при b = a и 0 при b > a. Таким образом, Д (1) является разрывной функцией от параметров a и b. Дирихле использовал интеграл (1) в своих исследованиях о притяжении эллипсоидов. Впрочем, этот интеграл встречается ранее у Ж. Фурье, С. Пуассона и А. Лежандра.
2) Интеграл
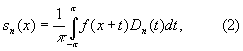
где
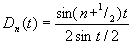
есть так называемое ядро Дирихле. Этот Д равен n-й частичной сумме
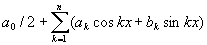
ряда Фурье функции f (х). Формула (2) является одной из важнейших формул теории рядов Фурье, в частности, позволившей Дирихле установить, что ряд Фурье функции, имеющей конечное число максимумов и минимумов, сходится в каждой точке.
3) Интеграл
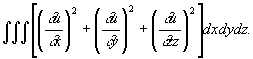
Подробнее см. Дирихле принцип (в теории гармонических функций).
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 05.03.2026 07:32:31
|

|

|
 |
|

|
 |
 |
 |
|