
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Деление (математич.) | Деление (далее Д) действие, обратное умножению; заключается в нахождении одного из двух сомножителей, если известны произведение их и др. сомножитель. Т. о., разделить а на b - это значит найти такое х, что bx = а или xb = а. Результат Д (математич.) х называется частным, или отношением, a и b. Заданное произведение а называется делимым, а заданный множитель b - делителем. Для обозначения Д (математич.) употребляют знаки двоеточия (а: b) или горизонтальной (иногда наклонной) черты (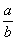 , a/b). , a/b).
В пределах системы целых чисел Д (математич.) не всегда возможно (6 делится на 2 и 3, но не делится на 5, см. Делимость), но в тех случаях, когда оно возможно, результат его всегда определен единственным образом (как говорят, однозначно). В системе всех рациональных чисел (т. е. чисел целых и дробных) Д (математич.) не только однозначно, но и всегда осуществимо, за единственным исключением - Д (математич.) на нуль. Если исходить из данного выше определения Д (математич.), то легко видеть, что Д (математич.) числа, отличного от нуля, на нуль невозможно. Результатом Д (математич.) нуля на нуль, по определению, может быть любое число (т.к. всегда с·0 = 0). Обычно в алгебре предпочитают (чтобы не нарушать однозначности Д (математич.)) считать, что Д (математич.) на нуль невозможно во всех случаях.
От точного Д (математич.), которое до сих пор рассматривалось, отличается Д (математич.) с остатком. Это, по существу, совершенно особая операция, отличная от Д (математич.) в определенном выше смысле. Если а и b - целые неотрицательные числа, то операция Д (математич.) с остатком числа а на число b состоит в определении целых неотрицательных чисел х и у, удовлетворяющих требованиям:
1) а = xb + у,
2) у < b.
При этом а называется делимым, b - делителем, х - частным, у - остатком. Эта операция всегда осуществима и всегда однозначна. Если у = 0, то говорят, что а делится на b без остатка. Аналогично определяется операция Д (математич.) с остатком для многочленов вида
(x) = a0xn + a1xn-1 +...+ an.
Она состоит в нахождении по двум многочленам Р(х) и Q(x) двух многочленов (x) и R(x), удовлетворяющих требованиям:
1) Р (х) = (x) Q (x) + R (x);
2) степень R (x) меньше степени Q (x). Эта операция также всегда осуществима и однозначна. Если R (x) º 0, то Р (х) делится на Q (x) без остатка.
Лит.: Депман И. Я., История арифметики, 2 изд., М., 1965; Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 13:11:05
|

|

|
 |
|

|
 |
 |
 |
|