
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Двойное отношение | Двойное отношение (далее Д) (сложное, или ангармоническое) четырех точек M1, M2, Мз, M4 на прямой (рис. 1), число, обозначаемое символом (M1M2M3M4) и равное
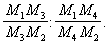
При этом отношение M1M3/M3M2 считается положительным, если направления отрезков M1M3 и M3M2 совпадают, и - отрицательным при различных направлениях. Д зависит от порядка нумерации точек, который может отличаться от порядка следования точек на прямой. Наряду с Д четырех точек, рассматривается Д четырех прямых, проходящих через точку О. Это отношение обозначается символом (m1m2m3m4). Оно равно
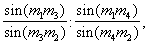
причем угол (mi mj) между прямыми mi и mj) рассматривается со знаком.
Если точки M1, M2, Мз, M4 лежат на прямых m1, m2, m3, m4 (рис. 1), то
(M1M2M3M4) = (m1m2m3m4),
поэтому, если точки M1, M2, Мз, M4 и M`1, M2`, Мз`, M4` получены пересечением одной четверки прямых m1, m2, m3, m4 (рис. 1), то (M1`, M2`, Мз`, M4`) = (M1M2M3M4).
Если же прямые m1, m2, m3, m4 и m1`, m2`, mз`, m4` проектируют одну четверку точек M1, M2, Мз, M4 (рис. 2), то (m1` m2` mз` m4`) = (m1m2m3m4).
Д не меняется также и при любых проективных преобразованиях, т. е. является инвариантом таких преобразований, и поэтому Д играют важную роль в проективной геометрии. Особенно важную роль играют четверки точек и прямых, для которых Д равно - 1. Такие четверки называют гармоническими (см. Гармоническое расположение.).
Э. Г. Позняк.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:56:31
|

|

|
 |
|

|
 |
 |
 |
|