
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Грина формулы | Грина формулы (далее Г) формулы интегрального исчисления, связывающие между собой интегралы различных типов. Простейшая из них связывает двойной интеграл по области G с криволинейным интегралом по границе С области G и имеет вид:
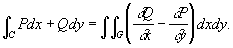
Эта формула была известна еще Л. Эйлеру (1771). Две другие впервые опубликованы Джорджем Грином в 1828 в связи с исследованиями по теории потенциала:
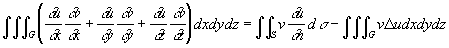
(первая Г, или предварительная Г) и
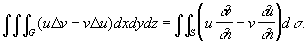
Здесь G - область трехмерного пространства, поверхность - граница этой области, Du = ¶2u/¶x2 + ¶2u/¶y2 + ¶2u/¶z2 (аналогично Dv) - оператор Лапласа, ¶u/¶n, ¶v/¶n - производные по направлению внешней нормали к .
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:16:45
|

|

|
 |
|

|
 |
 |
 |
|