График

График (далее Г) геометрическое изображение функциональной зависимости при помощи линии на плоскости. Например, на рис. 1 изображен Г изменения атмосферного давления со временем. Г применяют как для наглядного изображения функциональных зависимостей и придания наглядности их исследованию, так и для быстрого фактического нахождения значений функций по значениям аргументов. Виды Г очень разнообразны и зависят от того, какая система координат на плоскости положена в их основу. Если система координат выбрана, то Г функции f(x) есть не что иное, как множество (или, как иначе говорят, "геометрическое место") тех точек плоскости, координаты которых удовлетворяют уравнению y = f(x). В большинстве случаев Г строят в декартовых прямоугольных координатах. На рис. 2 изображен Г функции у = х2 — парабола, а на рис. 3 — Г функции 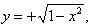 представляющий полуокружность, начинающуюся в точке с координатами (—1, 0) и кончающуюся в точке с координатами (+1, 0).   В прямоугольной системе координат масштабы по осям одинаковы; на практике от этого неудобного ограничения отказываются, выбирая разные масштабы по осям координат так, чтобы наилучшим образом использовать площадь листа бумаги, отводимую для Г Употребляются также Г, основанные на других системах координат, например полярной; последняя особенно удобна для изображения функций углового аргумента (на рис. 4 даны построенные в полярной системе координат Г распределения силы света, испускаемого по различным направлениям тремя типами дуговых фонарей). Иногда для упрощения вида Г целесообразно принимать за координаты точки те или иные функции от переменных х и у. (О возникающем отсюда особом способе графического изображения функций см. ст. Номография.) Например, если значениям аргумента и функции — значениям (х, у) — ставить в соответствие точку с декартовыми координатами (lgx, lgy), то Г функции у = хn при любом показателе n оказываются прямолинейными (рис. 5). Для быстрого вычерчивания подобных Г служит полулогарифмическая и логарифмическая бумага.   Если Г является прямой линией или дугой окружности, то его можно строить с помощью линейки или циркуля по двум, соответственно трем точкам. В остальных случаях для вычерчивания Г приходится наносить на бумагу достаточно большое число принадлежащих ему точек, а затем проводить через эти точки линию Г "на глаз". Эта операция, всегда несколько произвольная, во всяком случае имеет смысл лишь в предположении непрерывности функции. Если функция не только непрерывная, но и достаточно "гладкая" (т. е. ее производные первых двух-трех порядков меняются с изменением аргумента не слишком быстро), то при некотором навыке проведение Г по точкам делается очень точно. Нанеся на один чертеж Г функций y = j1(x) и y = j2(x), по точкам их пересечения можно определить корни уравнения j1(x) = j2(x) (см. рис. 3 в ст. Графические вычисления).   Существует большое число самопишущих приборов, автоматически наносящих на бумагу Г наблюдаемой функциональной зависимости, минуя ее аналитическое выражение (например, барограф, строящий Г давления атмосферы в функции времени). Часто для графического изображения зависимости между величинами пользуются диаграммами. В экономике и организации производства распространение получили контрольные и плановые Г (см. Графические методы в управлении производством) и организационные Г, изображающие организационные связи и зависимости (например, схема управления предприятием). Во многих вопросах целесообразно одновременно рассматривать Г нескольких различных функций, изображая их на одном и том же чертеже. Типичным примером таких Г являются графики движения на транспорте.