
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Алгебраическое число | Алгебраическое число (далее А) число а, удовлетворяющее алгебраическому уравнению a1an+ ... + акa +an+1 = 0, где n ³ 1, a1, ..., an, an+1 — целые (рациональные) числа. Число a называется целым А, если a1 = 1. Если многочлен f(x) = a1xn + ... + anx + an+1 не является произведением двух др. многочленов положительной степени с рациональными коэффициентом, то число n называется степенью А a. Простейшие А — корни двучленного уравнения xn = а, где а — рациональное число. Например, А будут рациональные числа, числа
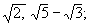
целыми А будут целые числа, числа
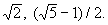
С понятием А тесно связаны два больших направления в теории чисел. 1) Арифметика А (алгебраическая теория чисел), созданная Э. Куммером в середине 19 в., изучает свойства А Целые А обладают рядом свойств, аналогичных свойствам целых рациональных чисел, однако теорема об единственности разложения числа на простые множители не имеет места в теории целых А Для сохранения единственности разложения Куммер ввел в рассмотрение т. н. "идеальные" числа (см. Идеал). 2) Теория приближения А изучает степень приближения А рациональными числами или алгебраическими же числами. Первым результатом в этом направлении была теорема Ж. Лиувилля, показывающая, что А "плохо" приближаются рациональными числами, точнее: если a - А степени n, то при любых целых рациональных р и q имеет место неравенство (a - p/q) > /qn, где С = С(a) > 0 — постоянная, не зависящая от р и q, отсюда следует, что легко построить произвольное количество неалгебраических — трансцендентных чисел.
Лит.: Гекке Э., Лекции по теории алгебраических чисел, пер. с нем., М. — Л., 1940; Гельфонд А. О., Трансцендентные и алгебраические числа, М., 1952; Боревич З. И., Шафаревич И. ., Теория чисел, М., 1964.
А. А. Карацуба. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 09.03.2026 22:22:38
|

|

|
 |
|

|
 |
 |
 |
|