
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Алгебраическая функция | Алгебраическая функция (далее А)функция, удовлетворяющая алгебраическому уравнению. Алгебраическая функция принадлежат к числу важнейших функций, изучаемых в математике. Из них многочлены и частные многочленов (например,
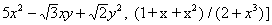
называются рациональными, а прочие Алгебраическая функция - иррациональными. Простейшими примерами последних могут служить Алгебраическая функция, выражаемые с помощью радикалов (например,
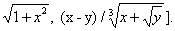
Однако существуют Алгебраическая функция, которые невозможно выразить через радикалы (например, функция у = f (х), удовлетворяющая уравнению: y5 + 3ух4 + x5 = 0). Примерами неалгебраических, т. н. трансцендентных функций, встречающихся в школьном курсе алгебры, являются: степенная xa (если a - иррациональное число), показательная ах, логарифмическая и т. д. Общая теория Алгебраическая функция представляет обширную математическую дисциплину, имеющую важные связи с теорией аналитических функций (Алгебраическая функция составляют специальный класс аналитических функций), алгеброй и алгебраической геометрией. Самая общая Алгебраическая функция многих переменных u = f(x, у, z, ...) определяется как функция, удовлетворяющая уравнению вида:
Ро(х, у, z, ...)un + 1(x, y, z, ...)un-1 + … +n(x, y, z, ...) = 0, (1)
где Р0, Р1, ..., n - какие-либо многочлены относительно х, у, z,... . Все выражение, стоящее в левой части, представляет некоторый многочлен относительно х, у, z,... и n. Его можно считать неприводимым, т. е. не разлагающимся в произведение многочленов более низких степеней; кроме того, многочлен 0 можно считать не равным тождественно нулю. Если n = 1, то u представляет рациональную функцию (u = -1/0), частным случаем которой - целой рациональной функцией - является многочлен (если 0 = const ¹ 0). При n > 1 получается иррациональная функция; если n = 2, то она выражается через многочлены с помощью квадратного корня; если n = 3 или n = 4, то для u получается выражение, содержащее квадратные и кубические корни.
При n ³ 5 число каких бы то ни было корней из многочленов. Иррациональная Алгебраическая функция всегда многозначна, а именно (при наших обозначениях и предположениях) является n-значной аналитической функцией переменных х, у, z,...
Лит.: Чеботарев Н. Г., Теория алгебраических функций, М. - Л., 1948. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 09.03.2026 22:21:42
|

|

|
 |
|

|
 |
 |
 |
|