|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Гипергеометрический ряд | Гипергеометрический ряд (далее Г), ряд вида
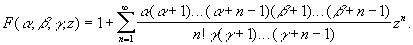
Г был впервые изучен Л. Эйлером (1778). Разложение многих функций в бесконечные ряды представляет собой частные случаи Г Например:
(1 + z) n = (—n, b; b; —z),
ln (1 + z) = z (1, 1; 2; —z),
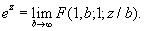
Г имеет смысл, если g не равно нулю или целому отрицательному числу; он сходится при |z| < 1. Если, кроме того, g—a—b >0, то Г сходится и при z = 1. В этом случае справедлива формула Гаусса:
(a, b; g; 1) = G(g)G(g—a—b)/G(g—a)G(g—b),
где Г (z) — гамма-функция. Аналитическая функция, определяемая для |z| < 1 с помощью Г, называется гипергеометрической функцией и играет важную роль в теории дифференциальных уравнений. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 03.12.2024 20:38:31
|
|
|
|
|
|
|
|
|
|
|
