
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Гиббса распределение | Гиббса распределение (далее Г), фундаментальный закон статистической физики, определяющий вероятность данного микроскопического состояния системы, т. е. вероятность того, что координаты и импульсы частиц системы имеют определенные значения.
Для систем, находящихся в тепловом равновесии с окружающей средой, в которой поддерживается постоянная температура (с термостатом), справедливо каноническое Г, установленное Дж. У. Гиббсом в 1901 для классической статистики. Согласно этому распределению, вероятность определенного микроскопического состояния пропорциональна функции распределения f (qi, pi), зависящей от координат qi и импульсов pi частиц системы:
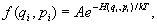
где (qi, pi) — функция Гамильтона системы, т. е. ее полная энергия, выраженная через координаты и импульсы частиц, k — Больцмана постоянная, Т — абсолютная температура; постоянная А не зависит от qi и pi и определяется из условия нормировки (сумма вероятностей пребывания системы во всех возможных состояниях должна равняться единице). Т. о., вероятность микросостояния определяется отношением энергии системы к величине kT (которая является мерой интенсивности теплового движения молекул) и не зависит от конкретных значений координат и импульсов частиц, реализующих данное значение энергии.
В квантовой статистике вероятность wn данного микроскопического состояния определяется значением энергетического уровня системы Eп.
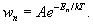
Для идеального газа, т. е. газа. в котором энергией взаимодействия частиц можно пренебречь, каноническое Г переходит в Больцмана распределение, определяющее вероятность того, что координата и импульс (энергия) отдельной частицы имеют данные значения (см. Больцмана статистика).
Если система изолирована, то ее энергия постоянна; в этом случае справедливо микроканоническое Г, согласно которому все микроскопические состояния изолированной системы равновероятны. Микроканоническое Г лежит в основе Г канонического.
Лит. см. при статье Статистическая физика.
Г. Я. Мякишев. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 10.03.2026 01:32:52
|

|

|
 |
|

|
 |
 |
 |
|