
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Гаусса принцип | Гаусса принцип (далее Г), принцип наименьшего принуждения, один из вариационных принципов механики, согласно которому для механической системы с идеальными связями (см. Связи механические) из всех кинематически возможных, т. e. допускаемых связями, движении, начинающихся из данного положения и с данными начальными скоростями, истинным будет то движение, для которого "принуждение" Z является в каждый момент времени наименьшим. Установлен К. Гауссом (1829).
Физическая величина, называемая "принуждением", вводится следующим образом. Свободная материальная точка с массой m при действии на нее заданной силы будет иметь ускорение /m; если же на точку наложены связи, то ее ускорение при действии той же силы станет равным какой-то др. величине w. Тогда отклонение точки от свободного движения, вызванное действием связи, будет зависеть от разности этих ускорений, т. e. от /m-w. Величину Z, пропорциональную квадрату этой разности, и называют "принуждением". Для одной точки
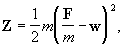
а для механической системы Z равняется сумме таких величин.
Рассмотрим, например, точку, которая начинает двигаться вдоль гладкой наклонной плоскости из положения А без начальной скорости (см. рис.). Для нее кинематически возможно любое перемещение АВ, AB1, AB2,... в этой плоскости с какими-то ускорениями w, w1, w2,..; при свободном же падении точка совершила бы перемещение AC вдоль вертикали с ускорением g. Тогда отклонения точки от свободного движения изобразятся отрезками , 1, 2,..., наименьшим из которых будет отрезок , перпендикулярный к наклонной плоскости. Следовательно, "принуждение" Z, пропорциональное квадратам , 1, 2,..., будет наименьшим при движении вдоль линии наименьшего ската AD. Это и будет истинное движение точки, происходящее с ускорением w = gsina.
Г пользуются для составления уравнений движения механических систем и изучения свойств этих движений.
Лит. см. при ст. Вариационные принципы механики.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 10.03.2026 01:39:16
|

|

|
 |
|

|
 |
 |
 |
|