
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Гамма-функция | Гамма-функция (далее Г) (Г-функция, Г (х)), одна из важнейших специальных функций, обобщающая понятие факториала; для целых положительных n равна Г (n) = (n - 1)! = 1·2... (n - 1). Впервые введена Л. Эйлером в 1729. Г-ф. для действительных х > 0 определяется равенством
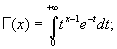
другое обозначение:
Г (х + 1) = p(x) = х!
Основные соотношения для Г-ф.:
Г (х + 1) = хГ (х) (функциональное уравнение);
Г (х) Г (1 - х) = p/sin px (формула дополнения);
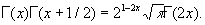
Частные значения:
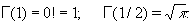
При больших х справедлива асимптотич. Стирлинга формула
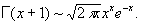
Через Г-ф. выражается большое число определенных интегралов, бесконечных произведений и сумм рядов. Г-ф. распространяется и на комплексные значения аргумента.
Лит.: Янке Е., Эмде Ф., Таблицы функций с формулами и кривыми, пер. с нем., 3 изд., М., 1959; Фихтенгольц Г М., Курс дифференциального и интегрального исчисления, 6 изд., т. 2, М., 1966. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 10.03.2026 00:06:14
|

|

|
 |
|

|
 |
 |
 |
|