|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Гамильтона оператор | Гамильтона оператор (далее Г)набла оператор, Ñ-оператор, дифференциальный оператор вида
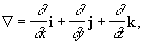
где i, j, k - координатные орты. Введен У. Р. Гамильтоном (1853). Если Гамильтона оператор применить к скалярной функции j(x, у, z), понимая Ñj как произведение вектора на скаляр, то получится градиент функции j(x, у, z):
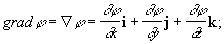
если применить Гамильтона оператор к векторной функции r (x, у, z), понимая Dr как скалярное произведение векторов, то получится дивергенция вектора r:
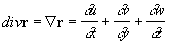
(u, v и w - координаты вектора r). Скалярное произведение Гамильтона оператор самого на себя дает Лапласа оператор.
 |
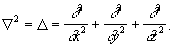Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 31.10.2025 17:44:17
|
|
|
|
|
|
|
|
|
|
|
