
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Активированный комплекс | Активированный комплекс (далее А)группировка в решающий момент элементарного акта реакции. Понятием об Активированный комплекс широко пользуются в теории скоростей реакций.
Протекание элементарного акта может быть рассмотрено на примере газовой бимолекулярной реакции образования из и паров иода:
2+2 = 2 (1)
Как показывает квантовомеханическая теория, при сближении молекул 2 и 2 на расстояние, сравнимое с молекулярными размерами, они отталкиваются друг от друга с силой, быстро растущей при уменьшении расстояния. Подавляющее большинство столкновений молекул 2 и 2 в газовой смеси не приводит к реакции, потому что энергия теплового движения молекул оказывается недостаточной для преодоления отталкивания. У некоторой, весьма малой, доли молекул интенсивность теплового движения случайно много больше средней; этим создается возможность настолько тесного сближения молекул 2 и 2, что возникают новые связи между Н и , а существовавшие прежде связи Н-Н и - разрываются. Две образовавшиеся молекулы отталкиваются друг от друга и поэтому расходятся, чем завершается элементарный акт реакции. Переход от расположения связей 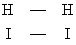 к расположению к расположению 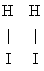 происходит не внезапно, а постепенно: по мере сближения молекул 2 и 2 связи Н-Н и - ослабевают и одновременно усиливаются связи Н-. Отталкивание Н-Н от - сменяется отталкиванием Н- от Н- в момент, когда новое расположение связей начинает превалировать над старым. Таким образом, в ходе элементарного акта возникает конфигурация являющаяся критической в том смысле, что если она достигнута, то дальнейшее движение происходит беспрепятственно, не требуя запаса энергии. Совокупность в этой конфигурации и называется "активированным комплексом" (Г. Эйринг, США, 1935) или "переходным состоянием" (М. Г. Эванс и М. Поляни, Англия, 1935). Для обратной реакции происходит не внезапно, а постепенно: по мере сближения молекул 2 и 2 связи Н-Н и - ослабевают и одновременно усиливаются связи Н-. Отталкивание Н-Н от - сменяется отталкиванием Н- от Н- в момент, когда новое расположение связей начинает превалировать над старым. Таким образом, в ходе элементарного акта возникает конфигурация являющаяся критической в том смысле, что если она достигнута, то дальнейшее движение происходит беспрепятственно, не требуя запаса энергии. Совокупность в этой конфигурации и называется "активированным комплексом" (Г. Эйринг, США, 1935) или "переходным состоянием" (М. Г. Эванс и М. Поляни, Англия, 1935). Для обратной реакции
2 = 2+2 (2)
расположение в Активированный комплекс будет таким же, как и для прямой реакции (1), но направления движения в активированных комплексах реакций (1) и (2) взаимно противоположны.
Энергетические соотношения при элементарном акте реакции можно схематически представить с помощью графика, на котором потенциальная энергия реагирующей системы изображена как функция т. н. реакционной координаты х, описывающей взаимное расположение
Задавшись некоторым весьма малым интервалом Dх (рис.) и считая, что конфигурация отвечает Активированный комплекс, если координата х имеет значение, лежащее в пределах этого интервала, можно ввести понятия - концентрация активированных комплексов прямой реакции в данной реагирующей системе с+ и их время жизни t. За время t в единице объема происходит с+ актов прямой реакции. Т. к. скорость прямой реакции r+. есть число соответствующих актов реакции в единице объема в единицу времени, то
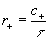 (3) (3)
Поскольку интервал Dх мал, то и с+ и t пропорциональны Dх, так что их отношение не зависит от значения произвольно выбранной величины Dх. Величины с+ и t вычисляются методами статистической механики, при этом используют ряд упрощающих предположений, из которых главным является допущение, что протекание реакции не нарушает статистически равновесное распределение молекул по состояниям.
Уравнение (3) выражает основную идею теоретической трактовки скоростей реакций на основе концепции Активированный комплекс Оно не только позволяет судить о зависимости скорости реакции от концентраций веществ - участников реакции, от температуры и др. факторов, но устанавливает абсолютное значение скорости. Поэтому метод Активированный комплекс часто называют теорией абсолютных скоростей реакций. В некоторых сравнительно немногочисленных реакциях перестройка связей происходит затрудненно, так что достижение конфигурации Активированный комплекс еще не гарантирует осуществление акта реакции. Чтобы учесть существование таких реакций, называемых неадиабатными, в правую часть равенства (3) вводят добавочный множитель, "коэффициент прохождения" или "трансмиссионный коэффициент"; в случае неадиабатных реакций он много меньше единицы.
Исходные понятия метода Активированный комплекс были разъяснены выше на примере гомогенной газовой реакции, но метод применяют и к скоростям реакций в растворах, гетерогенно-каталитических реакций и вообще к вычислению скоростей во всех случаях, когда превращение связано с необходимостью случайного концентрирования энергии теплового движения в количестве, значительно превышающем среднюю энергию молекул при данной температуре.
Сопоставление теории абсолютных скоростей реакций с опытными данными, как и теоретический анализ ее предпосылок, показывает, что эта теория, будучи не вполне точной, вместе с тем является удачным приближением, ценным своей простотой.
Лит.: Глесстон С., Лейдлер К., Эйринг Г., Теория абсолютных скоростей реакции, пер. с англ., М., 1948.
М. И. Темкин.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:45:14
|

|

|
 |
|

|
 |
 |
 |
|