Вычет

Вычет (далее В)1) в теории чисел. Число а называется вычетом числа b по модулю m, если разность а — b делится на m (a, b, m > 0 — целые числа). Например, число 24 есть Вычет числа 3 по модулю 7, так как 24—3 делится на 7. Совокупность m целых чисел, каждое из которых является Вычет одного и только одного из чисел 0, 1,..., m — 1, называется полной системой Вычет по модулю m. Например, числа 1, 6, 11, 16, 21, 26 образуют полную систему Вычет по модулю 6. Число а называется вычетом степени n (n ³ 2 — целое) по модулю m, если существует целое число х, такое, что разность xn — a делится на m. В противном случае а называется невычетом степени n. Например, 2 и 3, соответственно, вычет и невычет второй степени (квадратичные) по модулю 7.   Лит.: Виноградов И. М., Основы теории чисел, 7 изд. М., 1965.   А. А. Карацуба.   2) В теории аналитических функций вычетом однозначной аналитической функции f (z) относительно ее изолированной особой точки z0 называется коэффициент при (z — z0)-1 в разложении этой функции в ряд по степеням разности (z — z0) (Лорана ряд) в окрестности точки z0. Обозначение: выч f (z) (или res f (z)).         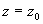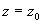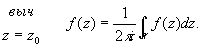Если g — окружность достаточно малого радиуса с центром в точке z0 (такая, что внутри нее функция f (z) не имеет особых точек, отличных от z0), то     Важное значение вычетов вытекает из следующей теоремы. 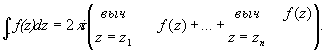Пусть f (z) — однозначная аналитическая функция в области D, за исключением изолированных особых точек, Г — простая замкнутая спрямляемая кривая, принадлежащая области D вместе со своей внутренностью и не проходящая через особые точки функции f (z); если z1,..., zn — все особые точки f (z), лежащие внутри Г, то     Поскольку вычеты вычисляются сравнительно просто, эта теорема является эффективным средством для нахождения интегралов.   Лит. см. при статье Аналитические функции.   А. А. Гончар.