
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Второе начало термодинамики | Второе начало термодинамики (далее В)принцип, устанавливающий необратимость макроскопических процессов, протекающих с конечной скоростью. В отличие от чисто механических (без трения) или электродинамических (без выделения джоу-левой теплоты) обратимых процессов, процессы, связанные с теплообменом при конечной разности температур (т. е. текущие с конечной скоростью), с трением, диффузией газов, расширением газов в пустоту, выделением джоулевой теплоты и т.д., необратимы, т. е. могут самопроизвольно протекать только в одном направлении (см. Необратимые процессы).
Исторически Второе начало термодинамики возникло из анализа работы тепловых машин (С. Карно, 1824). Существует несколько эквивалентных формулировок Второе начало термодинамики Само название "Второе начало термодинамики" и исторически первая его формулировка (1850) принадлежат Р. Клаузиусу: невозможен процесс, при котором теплота переходила бы самопроизвольно от тел более холодных к телам более нагретым. При этом самопроизвольный переход не следует понимать в узком смысле: невозможен не только непосредственный переход, его невозможно осуществить и с помощью машин или приборов без того, чтобы в природе не произошло еще каких-либо изменений. Иными словами, невозможно провести процесс, единственным следствием которого был бы переход теплоты от более холодного тела к более нагретому. Если бы (в нарушение положения Клаузиуса) такой процесс оказался возможным, то можно было бы, разделив один тепловой резервуар на 2 части и переводя теплоту из одной в другую, получить 2 резервуара с различными температурами. Это позволило бы, в свою очередь, осуществить Карно цикл и получить механическую работу с помощью периодически действующей (т. е. многократно возвращающейся к исходному состоянию) машины за счет внутренней энергии одного теплового резервуара. Поскольку это невозможно, в природе невозможны процессы, единственным следствием которых был бы подъем груза (т. е. механическая работа), произведенный за счет охлаждения теплового резервуара (такова формулировка Второе начало термодинамики, данная У. Томсоном, 1851). Обратно, если бы можно было получить механическую работу за счет внутренней энергии одного теплового резервуара (в противоречии с Второе начало термодинамики по Томсону), то можно было бы нарушить и положение Клаузиуса. Механическую работу, полученную за счет теплоты от более холодного резервуара, можно было бы использовать для нагревания более теплого резервуара (например, трением) и тем самым осуществить переход теплоты от холодного тела к нагретому. Обе приведенные формулировки Второе начало термодинамики, являясь эквивалентными, подчеркивают существенное различие в возможности реализации энергии, полученной за счет внешних источников работы, и энергии беспорядочного (теплового) движения частиц тела.
Возможность использования энергии теплового движения частиц тела (теплового резервуара) для получения механической работы (без изменения состояния других тел) означала бы возможность реализации так называемого вечного двигателя 2-го рода, работа которого не противоречила бы закону сохранения энергии. Так, работа двигателя корабля за счет охлаждения забортной воды океана - доступного и практически неисчерпаемого резервуара внутренней энергии - не противоречит закону сохранения энергии, но если, кроме охлаждения воды, нигде других изменений нет, то работа такого двигателя противоречит Второе начало термодинамики В реальном тепловом двигателе процесс превращения теплоты в работу обязательно сопряжен с передачей определенного количества теплоты внешней среде. В результате тепловой резервуар двигателя охлаждается, а более холодная внешняя среда нагревается, что находится в согласии со Второе начало термодинамики Следовательно, Второе начало термодинамики можно формулировать и как невозможность вечного двигателя 2-го рода.
Г. А. Зисман.
В современной термодинамике Второе начало термодинамики формулируется единым и самым общим образом как закон возрастания особой функции состояния системы, которую Клаузиус назвал энтропией (обозначается ). Согласно этому закону, в замкнутой системе энтропия при любом реальном процессе либо возрастает, либо остается неизменной, т. е. изменение энтропии d ³ 0; знак равенства имеет место для обратимых процессов. В состоянии равновесия энтропия замкнутой системы достигает максимума и никакие макроскопические процессы в такой системе, согласно Второе начало термодинамики, невозможны. Для незамкнутой системы направление возможных процессов, а также условия равновесия могут быть получены из закона возрастания энтропии, примененного к составной замкнутой системе, получаемой путем присоединения всех тел, участвующих в процессе. Это приводит в общем случае необратимых процессов к неравенствам
 dQ £ TdS, (1) dQ £ TdS, (1)
dU - TdS - dA £ 0, (1¢)
где dQ - переданное системе количество теплоты, dА - совершенная над ней работа, d - изменение ее внутренней энергии, Т - абсолютная температура; знак равенства относится к обратимым процессам.
Важные следствия дает применение Второе начало термодинамики к системам, находящимся в фиксированных внешних условиях. Например, для систем с фиксированной температурой и объемом неравенство (1¢) приобретает вид d £ 0, где = - TS -свободная энергия системы. Таким образом, в этих условиях направление реальных процессов определяется убыванием свободной энергии, а состояние равновесия - минимумом этой величины (см. Потенциалы термодинамические).
Приведенные в начале статьи формулировки Второе начало термодинамики являются частным следствием общего закона возрастания энтропии.
Второе начало термодинамики, несмотря на свою общность, не имеет абсолютного характера, и отклонения от него (флуктуации) являются вполне закономерными. Примерами таких флуктуационных процессов являются броуновское движение тяжелых частиц, равновесное тепловое излучение нагретых тел (в том числе радиошумы), возникновение зародышей новой фазы при фазовых переходах, самопроизвольные флуктуации температуры и давления в равновесной системе и т.д.
Статистическая физика, построенная на анализе микроскопического механизма явлений, происходящих в макроскопических телах, и выяснившая физическую сущность энтропии, позволила понять природу Второе начало термодинамики, определить пределы его применимости и устранить кажущееся противоречие между механической обратимостью любого, сколь угодно сложного микроскопического процесса и термодинамической необратимостью процессов в макротелах.
Как показывает статистическая термодинамика (Л. Больцман, Дж. Гиббс), энтропия системы связана со статистическим весом Р макроскопического состояния:
= kln (k - Больцмана постоянная). Статистический вес Р пропорционален числу различных микроскопических реализаций данного состояния макроскопической системы (например, различных распределений значений координат и импульсов молекул газа, отвечающих определенному значению энергии, давления и других термодинамических параметров газа), т. е. характеризует как бы степень неточности микроскопического описания макросостояния. Для замкнутой системы вероятность термодинамическая данного макросостояния пропорциональна его статистическому весу и определяется энтропией системы:
~ exp (/k). (2)
Таким образом, закон возрастания энтропии имеет статистически-вероятностный характер и выражает постоянную тенденцию системы к переходу в более вероятное состояние. Максимально вероятным является состояние равновесия; за достаточно большой промежуток времени любая замкнутая система достигает этого состояния.
Энтропия является величиной аддитивной (см. Аддитивность), она пропорциональна числу частиц в системе. Поэтому для систем с большим числом частиц даже самое ничтожное относительное изменение энтропии, приходящейся на одну частицу, существенно меняет ее абсолютную величину; изменение же энтропии, стоящей в показателе экспоненты в ур-нии (2), приводит к изменению вероятности данного макросостояния в огромное число раз. Именно этот факт является причиной того, что для системы с большим числом частиц следствия Второе начало термодинамики практически имеют не вероятностный, а достоверный характер. Крайне маловероятные процессы, сопровождающиеся сколько-нибудь заметным уменьшением энтропии, требуют столь огромных времен ожидания, что их реализация является практически невозможной. В то же время малые части системы, содержащие небольшое число частиц, испытывают непрерывные флуктуации, сопровождающиеся лишь небольшим абсолютным изменением энтропии. Средние значения частоты и размеров этих флуктуаций являются таким же достоверным следствием статистической термодинамики, как и само Второе начало термодинамики
Проиллюстрируем сказанное примером, позволяющим оценить масштабы величин, определяющих точность Второе начало термодинамики и отклонения от него. Рассмотрим флуктуационный процесс, в результате которого частиц, первоначально занимающих объем , равный 1 мкм3 (т. е. 10-18 м3), сконцентрируется самопроизвольно в половине этого объема. Отношение статистических весов начального (1) и конечного (2) состояний:
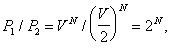
поэтому изменение энтропии D/k = in2 и отношение вероятностей 1/2 = 2. Если время пролета частицы через объем , т. е. время, в течение которого сохраняется данная флуктуация, t = 10-8 сек, то среднее время ожидания такой флуктуации t =2·t " 100,3·t. При числе частиц = 30, t = 10 сек, при = 100, t " 1022 сек " 1015 лет. Если же учесть, что при атмосферное давлении число частиц газа в 1 мкм3 составляет ~ 108, то время ожидания указанного события
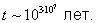
Буквальное применение Второе начало термодинамики к Вселенной как целому, приведшее Клаузиуса к неправильному выводу о неизбежности "тепловой смерти Вселенной", является неправомерным, так как любая сколь угодно большая часть Вселенной не является сама по себе замкнутой и ее приближение к состоянию теплового равновесия, даже не говоря о флуктуациях, не является абсолютным.
Термодинамическое же описание Вселенной как целого возможно лишь в рамках общей теории относительности, в которой вывод о приближении энтропии к максимуму не имеет места.
И. М. Лифшиц.
Лит.: Планк М., Введение в теоретическую физику, 2 изд., ч. 5, М. - Л., 1935; Френкель Я. И., Статистическая физика, М. - Л., 1948; Ландау Л., Лифшиц Е., Статистическая физика, М. - Л., 1951; Леонтович М. А., Введение в термодинамику, 2 изд., М. - Л., 1952; Самойлович А. Г., Термодинамика и статистическая физика, М., 1953; Смолуховский М., Границы справедливости второго начала термодинамики, "Успехи физических наук", 1967, т. 93, в. 4. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:49:13
|

|

|
 |
|

|
 |
 |
 |
|