
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Возрастание и убывание функции | Возрастание и убывание функции (далее В), функция y = f (x) называется возрастающей на отрезке (a, b), если для любой пары точек х и х", а £ х < х" £ b выполняется неравенство f (x) £ f (x"), и строго возрастающей — если выполняется неравенство f (x) < f (x"). Аналогично определяется убывание и строгое убывание функции. Например, функция у = х2 (рис., а) строго возрастает на отрезке (0,1), а
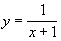
(рис., б) строго убывает на этом отрезке. Возрастающие функции обозначаются f (x), а убывающие f (x)¯. Для того чтобы дифференцируемая функция f (x) была возрастающей на отрезке (а, b), необходимо и достаточно, чтобы ее производная f"(x) была неотрицательной на (а, b).
Наряду с возрастанием и убыванием функции на отрезке рассматривают возрастание и убывание функции в точке. Функция у = f (x) называется возрастающей в точке x0, если найдется такой интервал (a, b), содержащий точку x0, что для любой точки х из (a, b), х> x0, выполняется неравенство f (x0) £ f (x), и для любой точки х из (a, b), х< x0, выполняется неравенство f (x) £ f (x0). Аналогично определяется строгое возрастание функции в точке x0. Если f"(x0) > 0, то функция f (x) строго возрастает в точке x0. Если f (x) возрастает в каждой точке интервала (a, b), то она возрастает на этом интервале.
Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 6 изд., т. 1, М., 1966.
С. Б. Стечкин.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:49:03
|

|

|
 |
|

|
 |
 |
 |
|