Вектор

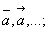
Вектор (далее В) (от лат. vector, буквально — несущий, перевозящий), в геометрическом смысле — направленный отрезок, то есть отрезок, у которого указаны начало (называемое также точкой приложения В) и конец. Для обозначения В используются либо жирные латинские буквы а, b, либо буквы обычного алфавита с черточками или стрелками наверху:     В, имеющий начало в точке А и конец в точке В, обозначается 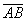. Прямая, на которой расположен В, называется линией действия данного В   Понятие В возникло в связи с изучением величин, характеризуемых численным значением и направленностью (например, перемещение, скорость и ускорение движущейся материальной точки, действующая на нее сила и т.п.). В механике и физике рассматривают свободные, скользящие и связанные В В называется свободным, если его значение не меняется при произвольном параллельном переносе. Свободным В является, например, скорость движения материальной точки. В называется скользящим, если его значение не меняется при любом параллельном переносе вдоль линии его действия. Примером скользящего В может служить сила, действующая на абсолютно твердое тело (две равные и расположенные на одной прямой силы оказывают на абсолютно твердое тело одинаковое воздействие). В называется связанным, если фиксировано его начало. Например, сила, приложенная к некоторой точке упругого тела, представляет собой связанный В Свойства свободных В изучаются средствами векторной алгебры (см. Вное исчисление). Общее понятие В как элемента, так называемого, векторного пространства определяется аксиоматически.   Лит.: Ильин В А., Позняк Э. Г., Аналитическая геометрия, М., 1968.   Э. Г. Позняк.